Los fenómenos y procesos naturales que nos rodean son bastante complejos. Para su descripción física exacta, se debe utilizar un aparato matemático engorroso y se debe tener en cuenta una gran cantidad de factores significativos. Para evitar este problema, en física se utilizan algunos modelos simplificados, que facilitan mucho el análisis matemático del proceso, pero prácticamente no afectan la precisión de su descripción. Uno de ellos es el modelo de gas ideal. Considerémoslo con más detalle en el artículo.
El concepto de gas ideal
Un gas ideal es un estado de agregación de una sustancia, que consta de puntos materiales que no interactúan entre sí. Expliquemos esta definición con más detalle.
Primero, estamos hablando de puntos materiales como objetos que forman un gas ideal. Esto significa que sus moléculas y átomos no tienen un tamaño, pero tienen una masa determinada. es audazse puede hacer una aproximación teniendo en cuenta que en todos los gases reales a bajas presiones y altas temperaturas, la distancia entre las moléculas es mucho mayor que sus dimensiones lineales.
En segundo lugar, las moléculas de un gas ideal no deben interactuar entre sí. En realidad, tales interacciones siempre existen. Entonces, incluso los átomos de los gases nobles experimentan una atracción dipolo-dipolo. En otras palabras, las interacciones de van der Waals están presentes. Sin embargo, en comparación con la energía cinética del movimiento de rotación y traslación de las moléculas, estas interacciones son tan pequeñas que no afectan las propiedades de los gases. Por lo tanto, no se pueden considerar al resolver problemas prácticos.
Es importante tener en cuenta que no todos los gases en los que la densidad es baja y la temperatura es alta pueden considerarse ideales. Además de las interacciones de van der Waals, existen otros tipos de enlaces más fuertes, por ejemplo, enlaces de hidrógeno entre moléculas H2O, que conducen a una grave violación de las condiciones de idealidad del gas. Por esta razón, el vapor de agua no es un gas ideal, pero el aire sí lo es.
Modelo físico de un gas ideal
Este modelo se puede representar de la siguiente manera: supongamos que el sistema de gas contiene N partículas. Estos pueden ser átomos y moléculas de varios químicos y elementos. El número de partículas N es grande, por lo que se suele utilizar la unidad "mol" para describirlo (1 mol corresponde al número de Avogadro). Todos se mueven en algún volumen V. Movimientos de partículasson caóticos e independientes entre sí. Cada uno de ellos tiene una cierta velocidad v y se mueve a lo largo de una trayectoria recta.
Teóricamente, la probabilidad de colisión entre partículas es casi cero, ya que su tamaño es pequeño en comparación con las distancias entre partículas. Sin embargo, si ocurre tal colisión, entonces es absolutamente elástica. En este último caso, se conservan el momento total de las partículas y su energía cinética.
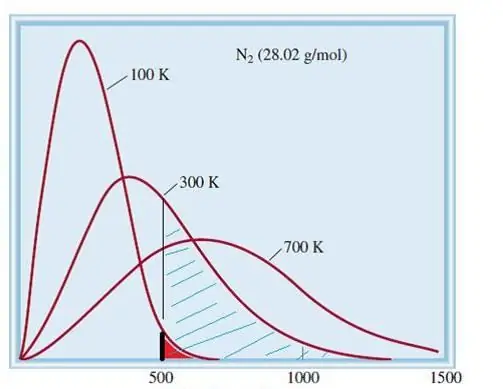
El modelo considerado de gases ideales es un sistema clásico con una gran cantidad de elementos. Por tanto, la velocidad y la energía de las partículas en él obedecen a la distribución estadística de Maxwell-Boltzmann. Algunas partículas tienen velocidades bajas, mientras que otras tienen velocidades altas. En este caso, existe un cierto límite de velocidad estrecho, en el que se encuentran los valores más probables de esta cantidad. La distribución de velocidades de las moléculas de nitrógeno se muestra esquemáticamente a continuación.
Teoría cinética de los gases
El modelo de gases ideales descrito anteriormente determina únicamente las propiedades de los gases. Este modelo fue propuesto por primera vez por Daniel Bernoulli en 1738.

Posteriormente, fue desarrollado hasta su estado actual por August Kroenig, Rudolf Clausius, Mikhail Lomonosov, James Maxwell, Ludwig Boltzmann, Marian Smoluchowski y otros científicos.
La teoría cinética de las sustancias fluidas, a partir de la cual se construye el modelo de gas ideal, explica dos importantes propiedades macroscópicas del sistema en función de su comportamiento microscópico:
- La presión en los gases es el resultado de la colisión de las partículas con las paredes del recipiente.
- La temperatura en el sistema es el resultado de la manifestación del movimiento constante de moléculas y átomos.
Ampliamos ambas conclusiones de la teoría cinética.
Presión de gas
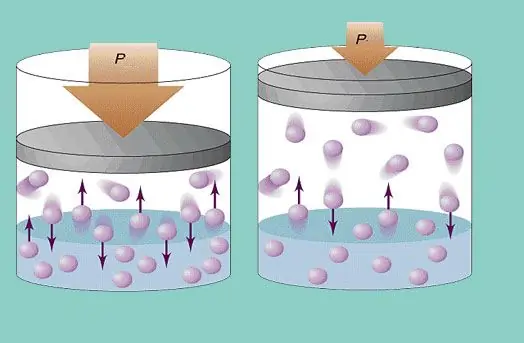
El modelo de gas ideal asume un movimiento caótico constante de partículas en el sistema y su colisión constante con las paredes del recipiente. Cada colisión de este tipo se considera absolutamente elástica. La masa de la partícula es pequeña (≈10-27-10-25 kg). Por lo tanto, no puede crear mucha presión en una colisión. Sin embargo, el número de partículas, y por lo tanto el número de colisiones, es enorme (≈1023). Además, la velocidad cuadrática media de la raíz de los elementos es de varios cientos de metros por segundo a temperatura ambiente. Todo esto conduce a la creación de una presión apreciable en las paredes del recipiente. Se puede calcular con la siguiente fórmula:
P=nortemetrovcp2 / (3V), donde vcp es la raíz cuadrática media de la velocidad, m es la masa de la partícula.
Temperatura absoluta
Según el modelo de gas ideal, la temperatura está determinada únicamente por la energía cinética promedio de una molécula o átomo en el sistema bajo estudio. Puedes escribir la siguiente expresión que relaciona la energía cinética y la temperatura absoluta de un gas ideal:
mvcp2 / 2=3 / 2kB T.
Aquí kB es la constante de Boltzmann. De esta igualdad obtenemos:
T=metro vcp2 / (3kB).
Ecuación universal de estado
Si combinamos las expresiones anteriores para la presión absoluta P y la temperatura absoluta T, podemos escribir la siguiente igualdad:
PV=norteRT.
Aquí n es la cantidad de sustancia en moles, R es la constante de los gases introducida por D. I. Mendeleev. Esta expresión es la ecuación más importante en la teoría de los gases ideales, porque combina tres parámetros termodinámicos (V, P, T) y no depende de las características químicas del sistema gaseoso.

La ecuación universal fue deducida experimentalmente por primera vez por el físico francés Emile Clapeyron en el siglo XIX y luego fue llevada a su forma moderna por el químico ruso Mendeleev, razón por la cual actualmente lleva los nombres de estos científicos.






