La Ley de Ohm es la ley básica de los circuitos eléctricos. Al mismo tiempo, nos permite explicar muchos fenómenos naturales. Por ejemplo, uno puede entender por qué la electricidad no "golpea" a los pájaros que se posan en los cables. Para la física, la ley de Ohm es extremadamente significativa. Sin su conocimiento, sería imposible crear circuitos eléctricos estables o no habría electrónica en absoluto.
Dependencia I=I(U) y su valor
La historia del descubrimiento de la resistencia de los materiales está directamente relacionada con la característica corriente-tensión. ¿Lo que es? Tomemos un circuito con una corriente eléctrica constante y consideremos cualquiera de sus elementos: una lámpara, una tubería de gas, un conductor de metal, un frasco de electrolito, etc.
Al cambiar el voltaje U (a menudo denominado V) suministrado al elemento en cuestión, rastrearemos el cambio en la intensidad de la corriente (I) que lo atraviesa. Como resultado, obtendremos una dependencia de la forma I \u003d I (U), que se denomina "característica de voltaje del elemento" y es un indicador directo de supropiedades eléctricas.
La característica V/A puede verse diferente para diferentes elementos. Su forma más simple se obtiene considerando un conductor de metal, que fue realizado por Georg Ohm (1789 - 1854).
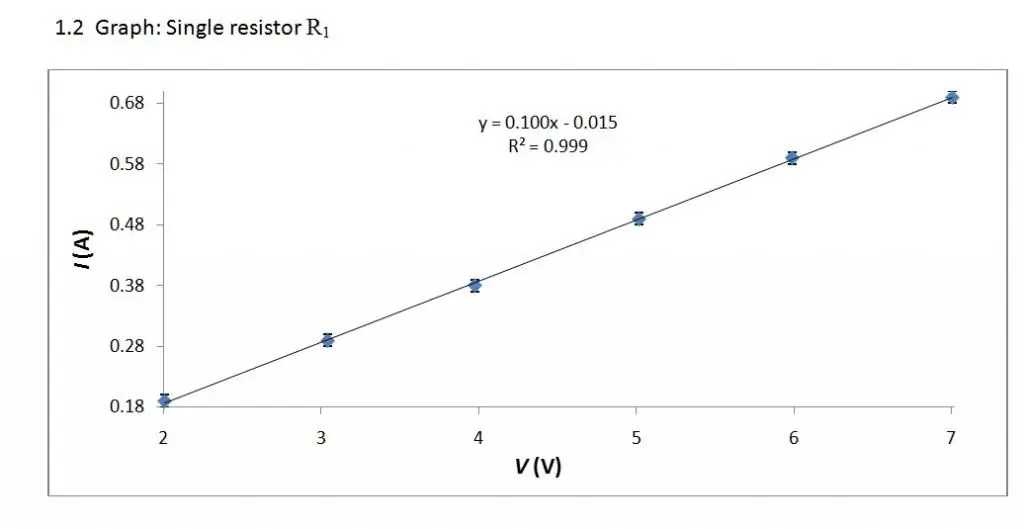
La característica de voltios-amperios es una relación lineal. Por lo tanto, su gráfica es una línea recta.
La ley en su forma más simple
La investigación de Ohm sobre las características de corriente-voltaje de los conductores mostró que la intensidad de la corriente dentro de un conductor metálico es proporcional a la diferencia de potencial en sus extremos (I ~ U) e inversamente proporcional a un determinado coeficiente, es decir, I ~ 1/R. Este coeficiente se conoció como "resistencia del conductor", y la unidad de medida de la resistencia eléctrica era Ohm o V/A.
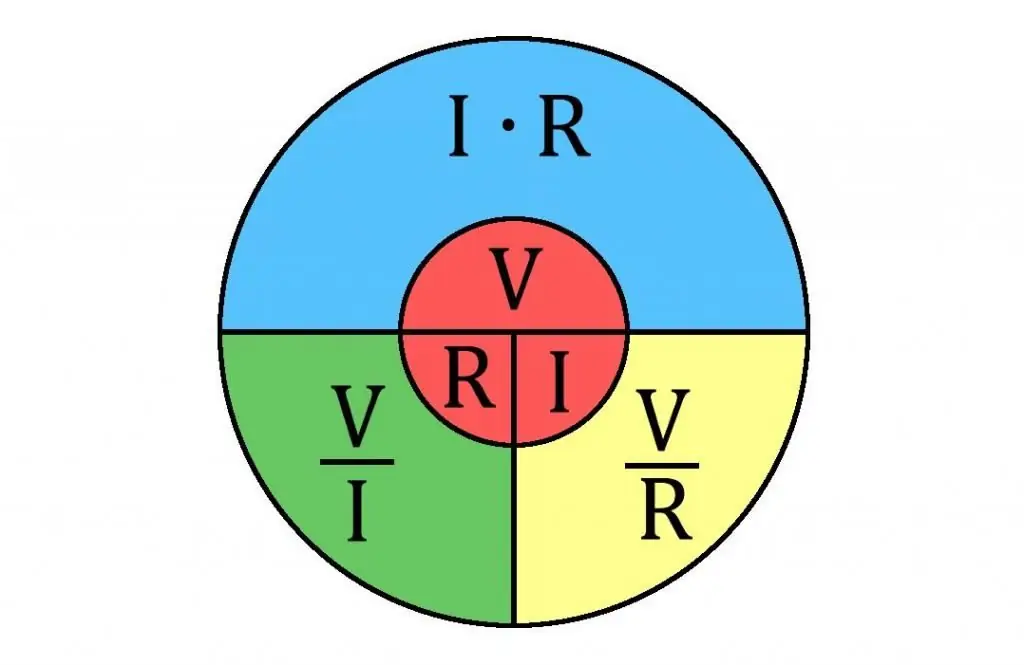
Una cosa más a tener en cuenta. La ley de Ohm se usa a menudo para calcular la resistencia en los circuitos.
Redacción de la ley
La ley de Ohm dice que la intensidad de corriente (I) de una sola sección del circuito es proporcional al voltaje en esta sección e inversamente proporcional a su resistencia.
Cabe señalar que de esta forma la ley sigue siendo válida solo para una sección homogénea de la cadena. Homogénea es aquella parte del circuito eléctrico que no contiene una fuente de corriente. A continuación se explicará cómo utilizar la ley de Ohm en un circuito no homogéneo.
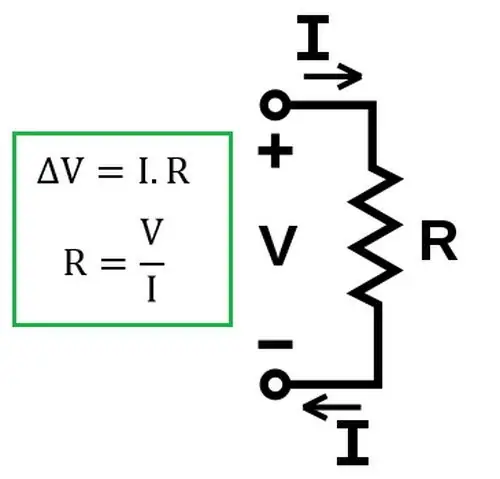
Más tarde, se estableció experimentalmente que la ley sigue siendo válida para las solucioneselectrolitos en un circuito eléctrico.
Significado físico de la resistencia
La resistencia es una propiedad de los materiales, sustancias o medios para impedir el paso de la corriente eléctrica. Cuantitativamente, una resistencia de 1 ohm significa que en un conductor con una tensión de 1 V en sus extremos, puede pasar una corriente eléctrica de 1 A.
Resistividad eléctrica
Experimentalmente, se encontró que la resistencia de la corriente eléctrica del conductor depende de sus dimensiones: largo, ancho, alto. Y también de su forma (esfera, cilindro) y del material del que está hecho. Así, la fórmula para la resistividad, por ejemplo, de un conductor cilíndrico homogéneo será: R \u003d pl / S.
Si en esta fórmula ponemos s=1 m2 y l=1 m, entonces R será numéricamente igual a p. A partir de aquí, se calcula la unidad de medida para el coeficiente de resistividad del conductor en el SI: esto es Ohmm.

En la fórmula de resistividad, p es el coeficiente de resistencia determinado por las propiedades químicas del material del que está hecho el conductor.
Para considerar la forma diferencial de la ley de Ohm, necesitamos considerar algunos conceptos más.
Densidad de corriente
Como saben, la corriente eléctrica es un movimiento estrictamente ordenado de cualquier partícula cargada. Por ejemplo, en los metales, los portadores de corriente son los electrones, y en los gases conductores, los iones.
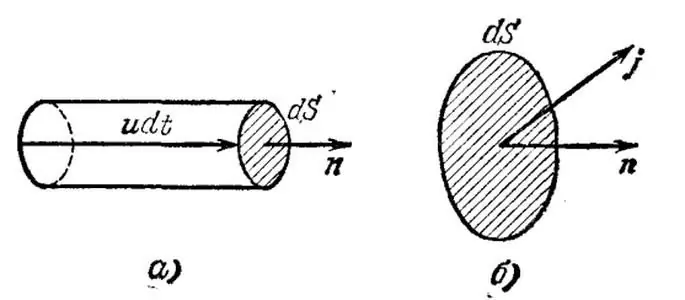
Tomemos el caso trivial cuando todos los operadores actualeshomogéneo - conductor metálico. Señalemos mentalmente un volumen infinitamente pequeño en este conductor y denotemos con u la velocidad promedio (deriva, ordenada) de los electrones en el volumen dado. Además, sea n la concentración de portadores de corriente por unidad de volumen.
Ahora dibujemos un área infinitesimal dS perpendicular al vector u y construyamos a lo largo de la velocidad un cilindro infinitesimal con una altura udt, donde dt denota el tiempo durante el cual pasarán todos los portadores de velocidad actuales contenidos en el volumen considerado por la zona dS
En este caso, la carga igual a q=neudSdt será transferida por electrones a través del área, donde e es la carga del electrón. Por lo tanto, la densidad de corriente eléctrica es un vector j=neu, que denota la cantidad de carga transferida por unidad de tiempo a través de una unidad de área.
Uno de los beneficios de la definición diferencial de la Ley de Ohm es que a menudo se puede pasar sin calcular la resistencia.
Carga eléctrica. Fuerza del campo eléctrico
La intensidad de campo junto con la carga eléctrica es un parámetro fundamental en la teoría de la electricidad. Al mismo tiempo, se puede obtener una idea cuantitativa de los mismos a partir de experimentos sencillos al alcance de los escolares.
Para simplificar, consideraremos un campo electrostático. Este es un campo eléctrico que no cambia con el tiempo. Tal campo puede ser creado por cargas eléctricas estacionarias.
Además, se necesita una carga de prueba para nuestros propósitos. En su capacidad usaremos un cuerpo cargado - tan pequeño que no es capaz de causarcualquier perturbación (redistribución de cargas) en los objetos circundantes.
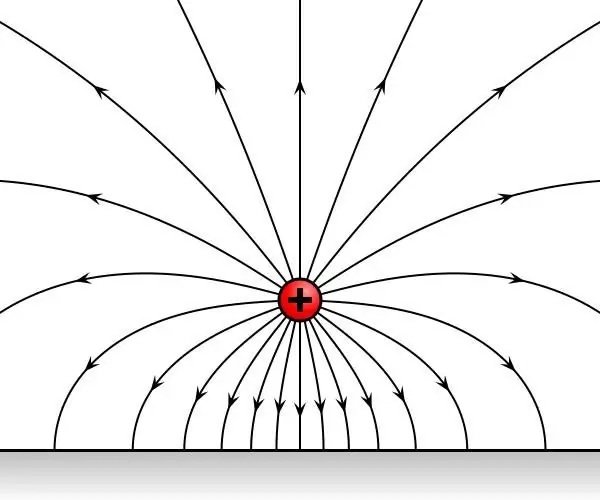
Considérense sucesivamente dos cargas de prueba tomadas, colocadas sucesivamente en un punto del espacio, que se encuentra bajo la influencia de un campo electrostático. Resulta que los cargos estarán sujetos a una influencia invariable en el tiempo de su parte. Sean F1 y F2 las fuerzas que actúan sobre las cargas.
Como resultado de la generalización de los datos experimentales, se encontró que las fuerzas F1 y F2 están dirigidas en una o en direcciones opuestas, y su relación F1/F2 es independiente del punto en el espacio donde se colocaron alternativamente las cargas de prueba. Por lo tanto, la relación F1/F2 es una característica de las propias cargas y no depende del campo.
El descubrimiento de este hecho permitió caracterizar la electrización de los cuerpos y más tarde se denominó carga eléctrica. Así, por definición, resulta q1/q2=F1/F 2 , donde q1 y q2 - la cantidad de cargas colocadas en un punto del campo, y F 1 y F2 - fuerzas que actúan sobre las cargas desde el lado del campo.
A partir de tales consideraciones, se establecieron experimentalmente las magnitudes de las cargas de varias partículas. Al establecer condicionalmente una de las cargas de prueba igual a uno en la relación, puede calcular el valor de la otra carga midiendo la relación F1/F2.
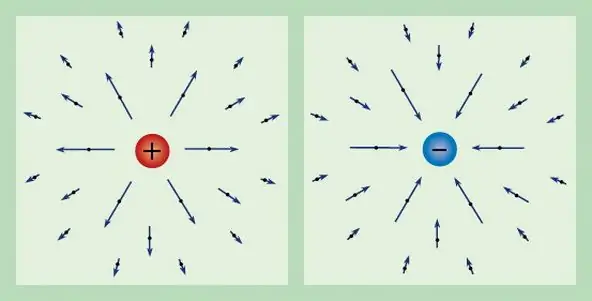
Cualquier campo eléctrico se puede caracterizar a través de una carga conocida. Por lo tanto, la fuerza que actúa sobre una unidad de carga de prueba en reposo se denomina intensidad de campo eléctrico y se denota por E. De la definición de la carga, obtenemos que el vector de fuerza tiene la siguiente forma: E=F/q.
Conexión de los vectores j y E. Otra forma de la ley de Ohm
En un conductor homogéneo, el movimiento ordenado de las partículas cargadas ocurrirá en la dirección del vector E. Esto significa que los vectores j y E estarán codirigidos. Al igual que para determinar la densidad de corriente, seleccionamos un volumen cilíndrico infinitamente pequeño en el conductor. Entonces, una corriente igual a jdS pasará a través de la sección transversal de este cilindro, y el voltaje aplicado al cilindro será igual a Edl. También se conoce la fórmula de la resistividad de un cilindro.
Entonces, escribiendo la fórmula de la intensidad de la corriente de dos formas, obtenemos: j=E/p, donde el valor 1/p se denomina conductividad eléctrica y es el inverso de la resistividad eléctrica. Por lo general, se denota σ (sigma) o λ (lambda). La unidad de conductividad es Sm/m, donde Sm es Siemens. Unidad inversa de Ohm.
Por lo tanto, podemos responder a la pregunta planteada anteriormente sobre la ley de Ohm para un circuito no homogéneo. En este caso, los portadores de corriente se verán afectados por la fuerza del campo electrostático, que se caracteriza por la intensidad E1, y otras fuerzas que actúan sobre ellos desde otra fuente de corriente, que puede ser designado E 2. Entonces se aplica la Ley de Ohm ala sección no homogénea de la cadena se verá así: j=λ(E1 + E2).
Más sobre conductividad y resistencia
La capacidad de un conductor para conducir una corriente eléctrica se caracteriza por su resistividad, que se puede encontrar a través de la fórmula de resistividad, o conductividad, calculada como el recíproco de la conductividad. El valor de estos parámetros está determinado tanto por las propiedades químicas del material conductor como por las condiciones externas. En particular, la temperatura ambiente.
Para la mayoría de los metales, la resistividad a temperatura normal es proporcional a ella, es decir, p ~ T. Sin embargo, se observan desviaciones a bajas temperaturas. Para una gran cantidad de metales y aleaciones a temperaturas cercanas a 0°K, el cálculo de la resistencia mostró valores cero. Este fenómeno se llama superconductividad. Por ejemplo, el mercurio, el estaño, el plomo, el aluminio, etc., tienen esta propiedad. Cada metal tiene su propia temperatura crítica Tk, a la que se observa el fenómeno de la superconductividad.
También tenga en cuenta que la definición de resistividad del cilindro se puede generalizar a cables hechos del mismo material. En este caso, el área de la sección transversal de la fórmula de resistividad será igual a la sección transversal del cable, y l - su longitud.






