Cuando se realiza una revisión por pares, por ejemplo, para evaluar la competitividad de los productos, es necesario, como en cualquier trabajo científico, llevar a cabo un procesamiento estadístico de datos. Este último comienza con la determinación de la consistencia de las opiniones de los expertos, cuya expresión numérica es el coeficiente de concordancia.
¿Por qué necesitamos una evaluación de consenso de expertos?
Esta evaluación es necesaria, en primer lugar, porque las opiniones de los expertos pueden diferir mucho sobre los parámetros estimados. Inicialmente, la evaluación se realiza ordenando los indicadores y asignándoles un determinado coeficiente de significación (peso). Una clasificación inconsistente hace que estos coeficientes sean estadísticamente poco confiables. Las opiniones de los expertos con su número requerido (más de 7-10) deben distribuirse de acuerdo con la ley normal.
El concepto del coeficiente de concordancia
Entonces. La consistencia es concordancia. El coeficiente es una cantidad adimensional que muestra la relación entre la dispersión y la dispersión máxima en el caso general. Generalicemos estos conceptos.
El coeficiente de concordancia es un número del 0 al 1, que muestra la consistencia de las opiniones de los expertos cuandoclasificar algunas propiedades. Cuanto más cerca esté este valor de 0, menor será la consistencia. Si el valor de este coeficiente es inferior a 0,3, las opiniones de los expertos se consideran inconsistentes. Cuando el valor del coeficiente está en el rango de 0,3 a 0,7, la consistencia se considera media. Un valor superior a 0,7 se considera de alta coherencia.
Casos de uso
Al realizar una investigación estadística, pueden surgir situaciones en las que un objeto puede caracterizarse no por dos secuencias, que se procesan estadísticamente utilizando el coeficiente de concordancia, sino por varias secuencias, que son clasificadas en consecuencia por expertos con el mismo nivel de profesionalismo en un área determinada.
Se debe determinar la consistencia de la clasificación realizada por expertos para confirmar la corrección de la hipótesis de que los expertos realizan mediciones relativamente precisas, lo que permite la formación de varias agrupaciones en grupos de expertos, que en gran medida están determinados por factores humanos, principalmente como las diferencias en puntos de vista, conceptos, diferentes escuelas científicas, la naturaleza de la actividad profesional, etc.
Breve descripción del método de clasificación. Sus ventajas y desventajas
Al clasificar, se utiliza el método de clasificación. Su esencia radica en el hecho de que a cada propiedad del objeto se le asigna su propio rango específico. Además, a cada experto incluido en el grupo de expertos, se le asigna este rangode manera independiente, resultando en la necesidad de procesar estos datos para identificar la consistencia de las opiniones de los expertos. Este proceso se lleva a cabo calculando el coeficiente de concordancia.
La principal ventaja del método de clasificación es su facilidad de implementación.
Las principales desventajas del método son:
- una pequeña cantidad de objetos de clasificación, ya que cuando su número excede de 15 a 20, se vuelve difícil asignar puntuaciones de clasificación objetivas;
- Basado en el uso de este método, la cuestión de qué tan lejos están los objetos estudiados entre sí en significado permanece abierta.
Al utilizar este método, se debe tener en cuenta que las calificaciones se basan en algún tipo de modelo probabilístico, por lo que se deben aplicar con cautela, dado el alcance.
Coeficiente de rango de concordancia de Kendall
Se utiliza para determinar la relación entre características cuantitativas y cualitativas que caracterizan objetos homogéneos y se clasifican según el mismo principio.
Este coeficiente está determinado por la fórmula:
t=2S/(n(n-1)), donde
S - la suma de las diferencias entre el número de secuencias y el número de inversiones en la segunda característica;
n - número de observaciones.

Algoritmo de cálculo:
- Los valores de x se clasifican en orden ascendente o descendente.
- Los valores de y se ordenan en el orden en que corresponden a los valores de x.
- Para cada rango sucesivo de y, determina cuántos valores de rango superior lo siguen. Se suman y se calcula la medida de correspondencia de secuencias de rangos en x e y.
- Del mismo modo, se calcula el número de rangos de y con valores más bajos, que también suman.
- Suma el número de rangos con valores más altos y el número de rangos con valores más bajos, lo que da como resultado el valor S.
Este coeficiente muestra la relación entre dos variables y, en la mayoría de los casos, se denomina coeficiente de correlación de rangos de Kendall. Dicha dependencia se puede representar gráficamente.
Determinación del coeficiente
¿Cómo se hace? Si el número de características o factores clasificados supera los 2, se utiliza el coeficiente de concordancia, que, en esencia, es una variante múltiple de la correlación de rangos.
Ten cuidado. El cálculo del coeficiente de concordancia se basa en la relación de la desviación de la suma de los cuadrados de los rangos de la suma promedio de los cuadrados de los rangos, multiplicada por 12, al cuadrado de los expertos, multiplicado por la diferencia entre el cubo del número de objetos y el número de objetos.
Algoritmo de cálculo
Para entender de dónde viene el número 12 en el numerador de la fórmula de cálculo, veamos el algoritmo de determinación.
Para cada línea con los rangos de un determinado experto, se calcula la suma de los rangos, que es un valor aleatorio.
El coeficiente de concordancia generalmente se define como la relación entre la estimación de la varianza (D) y el valor máximo de la estimación de la varianza(Dmax). Formulemos sucesivamente las definiciones de estas cantidades.
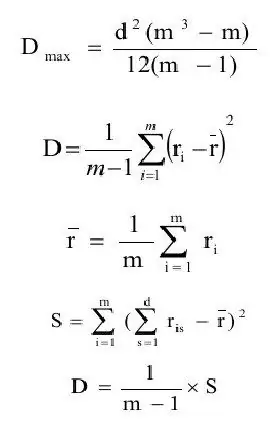
donde ravg - estimación de expectativas;
m - número de objetos.
Sustituyendo las fórmulas resultantes en relación a D por Dmax obtenemos la fórmula final para el coeficiente de concordancia:
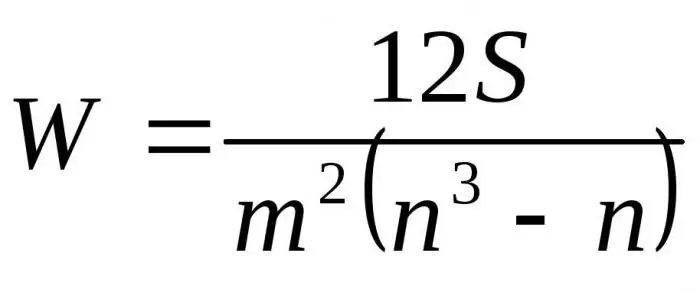
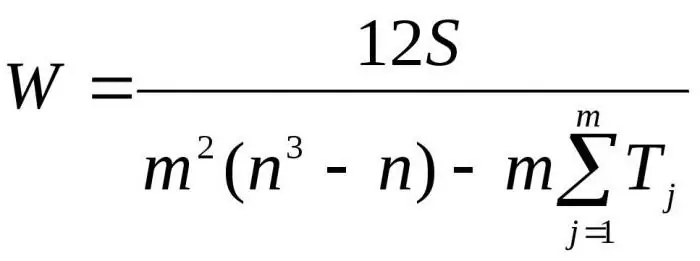
Aquí m es el número de expertos, n es el número de objetos.
La primera fórmula se usa para determinar el factor de concordancia si no hay rangos relacionados. La segunda fórmula se usa si hay rangos relacionados.
Entonces, el cálculo del coeficiente de concordancia ha terminado. ¿Que sigue? El valor obtenido se evalúa en cuanto a significancia utilizando el coeficiente de Pearson multiplicando este coeficiente por el número de expertos y por el número de grados de libertad (m-1). El criterio resultante se compara con el valor de la tabla, y si el valor del primero supera al último, hablan de la significación del coeficiente en estudio.
En el caso de rangos relacionados, el cálculo del criterio de Pearson se vuelve algo más complicado y se realiza mediante la siguiente relación: (12S)/(d(m2+ m)-(1/(m-1))x(Ts1 +Ts2 +Tsn)
Ejemplo
Suponga que el método experto evalúa la competitividad de la mantequilla que se vende en una red minorista. Demos un ejemplo de cálculo del coeficiente de concordancia. Antes de evaluar la competitividad, es necesario clasificar a los consumidorespropiedades de este producto que están involucradas en la evaluación. Supongamos que estas propiedades serán las siguientes: sabor y olor, consistencia y apariencia, color, empaque y etiquetado, contenido de grasa, nombre comercial, fabricante, precio.
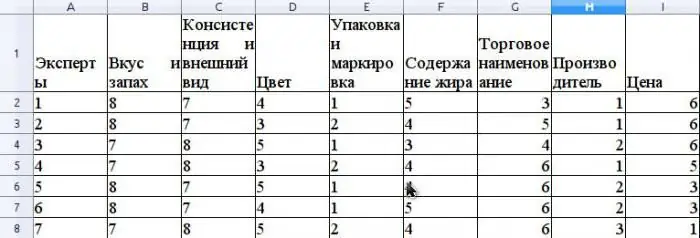
Suponga que el grupo de expertos consta de 7 expertos. La figura muestra los resultados de clasificar estas propiedades.
El valor promedio de r se calcula como el promedio aritmético y será 31,5. Para encontrar S, suma las diferencias al cuadrado entre ris y r promedio, según la fórmula arriba, y determine que el valor de S es 1718.
Calcule el coeficiente de concordancia usando la fórmula sin usar rangos relacionados (los rangos estarían relacionados si el mismo Asesor Experto tuviera los mismos rangos para diferentes propiedades).
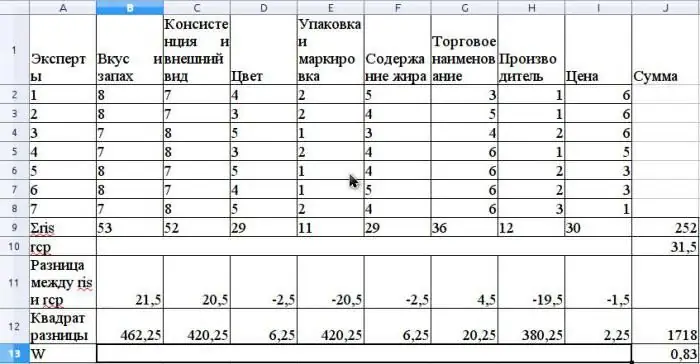
El valor de este coeficiente será 0,83. Esto indica un fuerte consenso entre los expertos.
Compruebe su significado usando la prueba de Pearson:
7 x 0,83 x (8-1)=40,7.
La prueba tabular de Pearson al 1% de nivel de significación es 18,5, y al 5% - 14,1..
El ejemplo demuestra la simplicidad y accesibilidad del cálculo para cualquier persona que conozca los conceptos básicos de los cálculos matemáticos. Para aliviarlos,utilizar formularios de hojas de cálculo.
En conclusión
Así, el coeficiente de concordancia muestra la consistencia de las opiniones de varios expertos. Cuanto más lejos esté de 0 y más cerca de 1, las opiniones más consistentes. Estos coeficientes deben confirmarse mediante el cálculo del criterio de Pearson.






