La resolución es la capacidad de un sistema de imágenes para reproducir los detalles de un objeto y depende de factores como el tipo de iluminación utilizada, el tamaño de píxel del sensor y las capacidades de la óptica. Cuanto menor sea el detalle del sujeto, mayor será la resolución requerida de la lente.
Introducción al proceso de resolución
La calidad de imagen de la cámara depende del sensor. En pocas palabras, un sensor de imagen digital es un chip dentro del cuerpo de una cámara que contiene millones de puntos sensibles a la luz. El tamaño del sensor de una cámara determina cuánta luz se puede usar para crear una imagen. Cuanto más grande sea el sensor, mejor será la calidad de la imagen ya que se recopila más información. Por lo general, las cámaras digitales se anuncian en el mercado para tamaños de sensor de 16 mm, Super 35 mm y, a veces, hasta 65 mm.
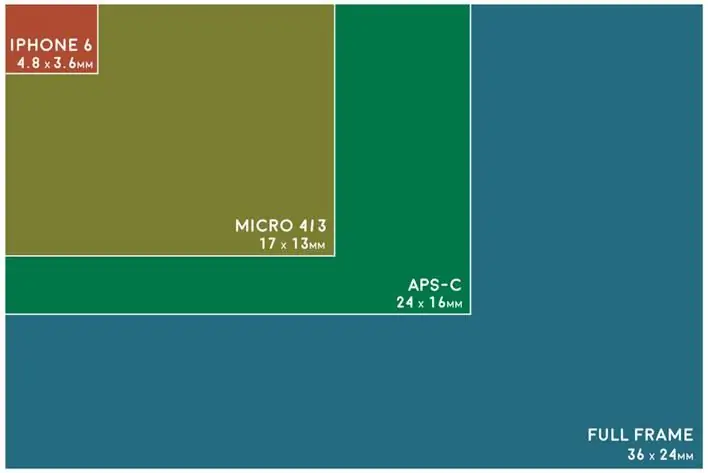
A medida que aumenta el tamaño del sensor, la profundidad de campo disminuirá en una apertura dada, ya que una contraparte más grande requiere que te acerques aobjeto o utilice una distancia focal más larga para llenar el encuadre. Para mantener la misma profundidad de campo, el fotógrafo debe utilizar aperturas más pequeñas.
Esta profundidad de campo reducida puede ser deseable, especialmente para lograr un desenfoque de fondo para retratos, pero la fotografía de paisajes requiere más profundidad, que es más fácil de capturar con el tamaño de apertura flexible de las cámaras compactas.
Dividir la cantidad de píxeles horizontales o verticales en un sensor indicará cuánto espacio ocupa cada uno en un objeto, y se puede usar para evaluar el poder de resolución de la lente y resolver las inquietudes de los clientes sobre el tamaño de píxel de la imagen digital del dispositivo. Como punto de partida, es importante comprender qué puede limitar realmente la resolución del sistema.
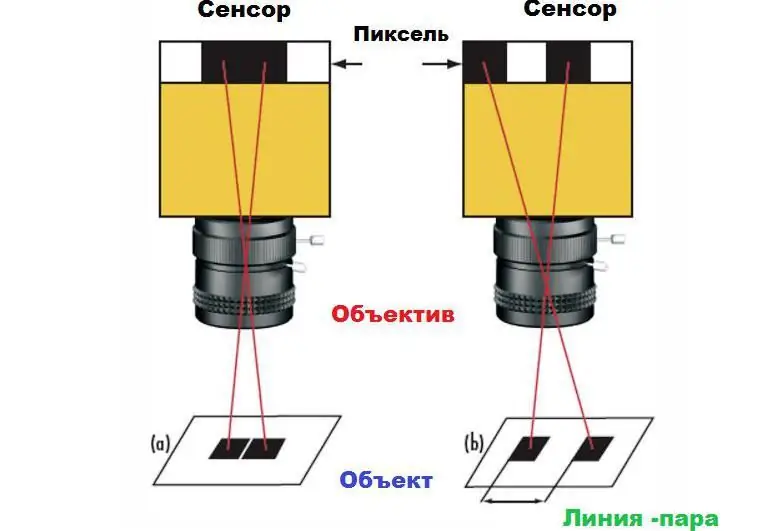
Esta afirmación se puede demostrar con el ejemplo de un par de cuadrados sobre un fondo blanco. Si los cuadrados del sensor de la cámara se asignan a píxeles vecinos, aparecerán como un gran rectángulo en la imagen (1a) en lugar de dos cuadrados separados (1b). Para distinguir los cuadrados, se requiere un cierto espacio entre ellos, al menos un píxel. Esta distancia mínima es la resolución máxima del sistema. El límite absoluto está determinado por el tamaño de los píxeles del sensor, así como por su número.
Medir las características de la lente
La relación entre cuadrados negros y blancos alternos se describe como un par lineal. Típicamente, la resolución está determinada por la frecuencia,medido en pares de líneas por milímetro - lp/mm. Desafortunadamente, la resolución de la lente en cm no es un número absoluto. A una resolución determinada, la capacidad de ver los dos cuadrados como objetos separados dependerá del nivel de la escala de grises. Cuanto mayor sea la separación de la escala de grises entre ellos y el espacio, más estable será la capacidad de resolver estos cuadrados. Esta división de la escala de grises se conoce como contraste de frecuencias.
La frecuencia espacial se da en lp/mm. Por esta razón, calcular la resolución en términos de lp/mm es extremadamente útil cuando se comparan lentes y se determina la mejor opción para determinados sensores y aplicaciones. El primero es donde comienza el cálculo de la resolución del sistema. Comenzando con el sensor, es más fácil determinar qué especificaciones de lente se necesitan para cumplir con los requisitos del dispositivo u otras aplicaciones. La frecuencia más alta permitida por el sensor, Nyquist, es efectivamente dos píxeles o un par de líneas.
La resolución de la lente de definición, también llamada resolución del espacio de imagen del sistema, se puede determinar multiplicando el tamaño en Μm por 2 para crear un par y dividiendo por 1000 para convertir a mm:
lp/mm=1000/ (2 X píxeles)
Los sensores con píxeles más grandes tendrán límites de resolución más bajos. Los sensores con píxeles más pequeños funcionarán mejor según la fórmula de resolución de lente anterior.
Área del sensor activo
Puedes calcular la resolución máxima para el objeto a servisita. Para ello, es necesario distinguir entre indicadores como la relación entre el tamaño del sensor, el campo de visión y el número de píxeles del sensor. El tamaño de este último se refiere a los parámetros del área activa del sensor de la cámara, generalmente determinados por el tamaño de su formato.
Sin embargo, las proporciones exactas variarán según la relación de aspecto, y los tamaños nominales de los sensores solo deben usarse como guía, especialmente para lentes telecéntricos y grandes aumentos. El tamaño del sensor se puede calcular directamente a partir del tamaño de píxel y el número activo de píxeles para realizar la prueba de resolución de la lente.
La tabla muestra el límite de Nyquist asociado con los tamaños de píxeles que se encuentran en algunos sensores de uso muy común.
| Tamaño de píxel (µm) | Límite de Nyquist acoplado (lp/mm) |
| 1, 67 | 299, 4 |
| 2, 2 | 227, 3 |
| 3, 45 | 144, 9 |
| 4, 54 | 110, 1 |
| 5, 5 | 90, 9 |
A medida que disminuye el tamaño de los píxeles, el límite de Nyquist asociado en lp/mm aumenta proporcionalmente. Para determinar el punto resoluble mínimo absoluto que se puede ver en un objeto, se debe calcular la relación entre el campo de visión y el tamaño del sensor. Esto también se conoce como aumento primario.(PMAG) sistemas.
La relación asociada al sistema PMAG permite escalar la resolución del espacio de la imagen. Por lo general, cuando se diseña una aplicación, no se especifica en lp/mm, sino en micras (µm) o fracciones de pulgada. Puede s altar rápidamente a la resolución final de un objeto utilizando la fórmula anterior para que sea más fácil elegir la resolución de la lente z. También es importante tener en cuenta que hay muchos factores adicionales, y la limitación anterior es mucho menos propensa a errores que la complejidad de tener en cuenta muchos factores y calcularlos mediante ecuaciones.
Calcular distancia focal
La resolución de una imagen es el número de píxeles que contiene. Designado en dos dimensiones, por ejemplo, 640X480. Los cálculos se pueden hacer por separado para cada dimensión, pero para simplificar esto a menudo se reduce a uno. Para realizar mediciones precisas en una imagen, debe usar un mínimo de dos píxeles para cada área más pequeña que desee detectar. El tamaño del sensor se refiere a un indicador físico y, por regla general, no se indica en los datos del pasaporte. La mejor manera de determinar el tamaño de un sensor es mirar los parámetros de píxeles en él y multiplicarlos por la relación de aspecto, en cuyo caso el poder de resolución de la lente resuelve los problemas de una mala toma.
Por ejemplo, la cámara Basler acA1300-30um tiene un tamaño de píxel de 3,75 x 3,75 um y una resolución de 1296 x 966 píxeles. El tamaño del sensor es de 3,75 µm x 1296 por 3,75 µm x 966=4,86 x 3,62 mm.
El formato del sensor se refiere al tamaño físico y no depende del tamaño de píxel. Este ajuste se utiliza paradeterminar con qué lente es compatible la cámara. Para que coincidan, el formato de la lente debe ser mayor o igual que el tamaño del sensor. Si se utiliza una lente con una relación de aspecto más pequeña, la imagen experimentará viñetas. Esto hace que las áreas del sensor fuera del borde del formato de la lente se oscurezcan.
Píxeles y selección de cámara

Para ver los objetos en la imagen, debe haber suficiente espacio entre ellos para que no se fusionen con los píxeles vecinos, de lo contrario serán indistinguibles entre sí. Si los objetos son de un píxel cada uno, la separación entre ellos también debe ser de al menos un elemento, es gracias a esto que se forma un par de líneas, que en realidad tiene un tamaño de dos píxeles. Esta es una de las razones por las que es incorrecto medir la resolución de cámaras y lentes en megapíxeles.
En realidad, es más fácil describir las capacidades de resolución de un sistema en términos de frecuencia de pares de líneas. De ello se deduce que a medida que disminuye el tamaño del píxel, la resolución aumenta porque puede colocar objetos más pequeños en elementos digitales más pequeños, tener menos espacio entre ellos y aun así resolver la distancia entre los sujetos que toma.
Este es un modelo simplificado de cómo el sensor de la cámara detecta objetos sin tener en cuenta el ruido u otros parámetros, y es la situación ideal.
Gráficos de contraste MTF
La mayoría de las lentes no son sistemas ópticos perfectos. La luz que pasa a través de una lente sufre un cierto grado de degradación. La cuestión es cómo evaluar este¿degradación? Antes de responder a esta pregunta, es necesario definir el concepto de "modulación". Este último es una medida de la lente de contraste en una frecuencia dada. Uno podría tratar de analizar imágenes del mundo real tomadas a través de una lente para determinar la modulación o el contraste de detalles de diferentes tamaños o frecuencias (espaciado), pero esto es muy poco práctico.
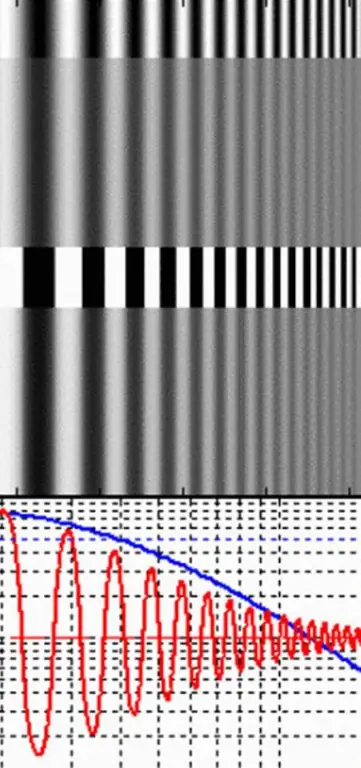
En cambio, es mucho más fácil medir la modulación o el contraste para pares de líneas blancas y oscuras alternas. Se llaman celosías rectangulares. El intervalo de líneas en una rejilla de ondas rectangular es la frecuencia (v), para la cual la función de modulación o contraste de la lente y la resolución se miden en cm.
La cantidad máxima de luz provendrá de las bandas claras y la mínima de las bandas oscuras. Si la luz se mide en términos de brillo (L), la modulación se puede determinar de acuerdo con la siguiente ecuación:
modulación=(Lmax - Lmin) / (Lmax + Lmin), donde: Lmax es el brillo máximo de las líneas blancas en la rejilla y Lmin es el brillo mínimo de las oscuras.
Cuando la modulación se define en términos de luz, a menudo se denomina contraste de Michelson porque toma la proporción de luminancia de las bandas claras y oscuras para medir el contraste.
Por ejemplo, hay una rejilla de onda cuadrada de cierta frecuencia (v) y modulación, y un contraste inherente entre las áreas oscuras y claras reflejadas desde esta rejilla a través de la lente. La modulación de la imagen y, por lo tanto, el contraste de la lente se mide para una frecuencia dadacompases (v).
La función de transferencia de modulación (MTF) se define como la modulación M i de la imagen dividida por la modulación del estímulo (objeto) M o, como se muestra en la siguiente ecuación.
|
MTF (v)=M i / M 0 |
USF se imprimen en papel láser brillante al 98 %. El tóner de impresora láser negro tiene una reflectancia de alrededor del 10 %. Así que el valor de M 0 es 88%. Pero dado que la película tiene un rango dinámico más limitado en comparación con el ojo humano, es seguro asumir que M 0 es esencialmente 100% o 1. Entonces, la fórmula anterior se reduce a lo siguiente más ecuación simple:
|
MTF (v)=Mi |
Entonces, la lente MTF para una frecuencia de rejilla dada (v) es simplemente la modulación de rejilla medida (Mi) cuando se fotografía a través de una lente en una película.
Resolución del microscopio
La resolución del objetivo de un microscopio es la distancia más corta entre dos puntos distintos en el campo de visión de su ocular que aún pueden distinguirse como objetos diferentes.
Si dos puntos están más cerca que su resolución, aparecerán borrosos y sus posiciones serán inexactas. El microscopio puede ofrecer una gran ampliación, pero si las lentes son de mala calidad, la mala resolución resultante degradará la calidad de la imagen.
Abajo está la ecuación de Abbe, donde la resoluciónla potencia del objetivo z de un microscopio es la potencia de resolución igual a la longitud de onda de la luz utilizada dividida por 2 (la apertura numérica del objetivo).
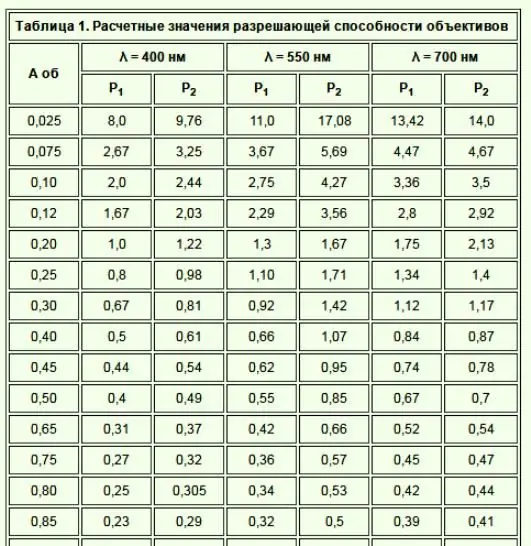
Varios elementos afectan la resolución de un microscopio. Un microscopio óptico ajustado a gran aumento puede producir una imagen borrosa, pero aún así tiene la resolución máxima de la lente.
La apertura digital de una lente afecta la resolución. El poder de resolución de un objetivo de microscopio es un número que indica la capacidad de una lente para captar luz y resolver un punto a una distancia fija del objetivo. El punto más pequeño que puede resolver la lente es proporcional a la longitud de onda de la luz recolectada dividida por el número de apertura numérica. Por lo tanto, un número mayor corresponde a una mayor capacidad de la lente para detectar un punto excelente en el campo de visión. La apertura numérica de la lente también depende de la cantidad de corrección de la aberración óptica.
Resolución de la lente del telescopio
Como un embudo de luz, un telescopio es capaz de recoger luz en proporción al área del agujero, esta propiedad es la lente principal.
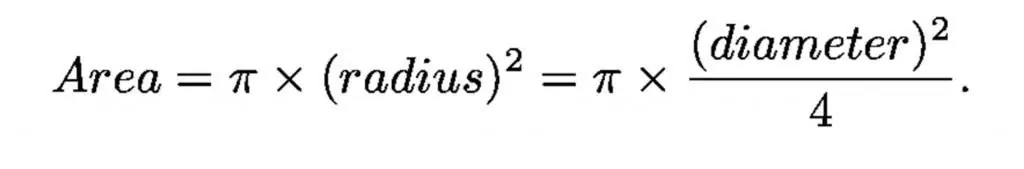
El diámetro de la pupila adaptada a la oscuridad del ojo humano es de poco menos de 1 centímetro, y el diámetro del telescopio óptico más grande es de 1000 centímetros (10 metros), por lo que el telescopio más grande es un millón de veces más grande en colección área que el ojo humano.

Es por eso que los telescopios ven objetos más débiles que los humanos. Y disponer de dispositivos que acumulen luz mediante sensores electrónicos de detección durante muchas horas.
Hay dos tipos principales de telescopio: refractores basados en lentes y reflectores basados en espejos. Los grandes telescopios son reflectores porque los espejos no tienen que ser transparentes. Los espejos de telescopio se encuentran entre los diseños más precisos. El error permitido en la superficie es aproximadamente 1/1000 del ancho de un cabello humano, a través de un orificio de 10 metros.
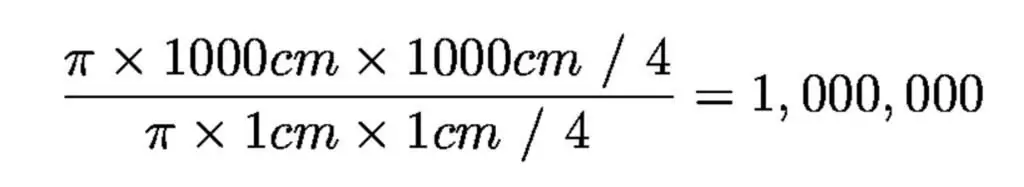
Los espejos solían estar hechos de enormes losas de vidrio grueso para evitar que se combaran. Los espejos de hoy son delgados y flexibles, pero están controlados por computadora o segmentados y alineados por control de computadora. Además de la tarea de encontrar objetos débiles, el objetivo del astrónomo también es ver sus detalles finos. El grado en que se pueden reconocer los detalles se denomina resolución:
- Imágenes borrosas=mala resolución.
- Imágenes claras=buena resolución.
Debido a la naturaleza ondulatoria de la luz y los fenómenos llamados difracción, el diámetro del espejo o la lente de un telescopio limita su resolución final en relación con el diámetro del telescopio. La resolución aquí significa el detalle angular más pequeño que se puede reconocer. Los valores pequeños corresponden a un excelente detalle de la imagen.
Los radiotelescopios deben ser muy grandes para proporcionar una buena resolución. La atmósfera de la Tierra esimágenes turbulentas y borrosas del telescopio. Los astrónomos terrestres rara vez pueden alcanzar la resolución máxima del aparato. El efecto turbulento de la atmósfera sobre una estrella se denomina visión. Esta turbulencia hace que las estrellas "parpadeen". Para evitar estos desenfoques atmosféricos, los astrónomos lanzan telescopios al espacio o los colocan en montañas altas con condiciones atmosféricas estables.
Ejemplos de cálculo de parámetros
Datos para determinar la resolución de la lente Canon:
- Tamaño de píxel=3,45 µm x 3,45 µm.
- Píxeles (Al x V)=2448 x 2050.
- Campo de visión deseado (horizontal)=100 mm.
- Límite de resolución del sensor: 1000/2x3, 45=145 lp/mm.
- Dimensiones del sensor: 3,45x2448/1000=8,45 mm3, 45x2050/1000=7,07 mm.
- PMAG:8, 45/100=0,0845 mm.
- Resolución de la lente de medición: 145 x 0,0845=12,25 lp/mm.
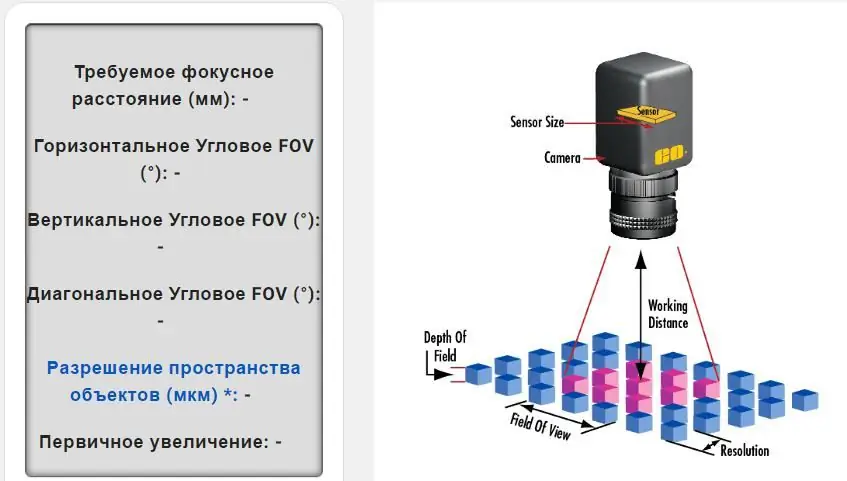
En realidad, estos cálculos son bastante complejos, pero lo ayudarán a crear una imagen basada en el tamaño del sensor, el formato de píxel, la distancia de trabajo y el campo de visión en mm. El cálculo de estos valores determinará la mejor lente para sus imágenes y aplicación.
Problemas de la óptica moderna

Desafortunadamente, duplicar el tamaño del sensor crea problemas adicionales para las lentes. Uno de los principales parámetros que afectan el costo de una lente de imagen es el formato. El diseño de una lente para un sensor de formato más grande requierenumerosos componentes ópticos individuales, que deberían ser más grandes y la transferencia del sistema más rígida.
Una lente diseñada para un sensor de 1" puede costar cinco veces más que una lente diseñada para un sensor de ½", incluso si no puede usar las mismas especificaciones con una resolución de píxeles limitada. El componente del costo debe considerarse antes de cómo para determinar el poder de resolución de una lente.
Las imágenes ópticas de hoy enfrentan más desafíos que hace una década. Los sensores con los que se utilizan tienen requisitos de resolución mucho más altos, y los tamaños de formato son simultáneamente más pequeños y más grandes, mientras que el tamaño de píxel sigue reduciéndose.
En el pasado, la óptica nunca limitaba el sistema de imágenes, hoy lo hace. Donde un tamaño de píxel típico es de alrededor de 9 µm, un tamaño mucho más común es de alrededor de 3 µm. Este aumento de 81x en la densidad de puntos ha pasado factura a la óptica y, aunque la mayoría de los dispositivos son buenos, la selección de lentes es ahora más importante que nunca.






