Los gases, desde el punto de vista de la termodinámica, se describen por un conjunto de características macroscópicas, siendo las principales la temperatura, la presión y el volumen. La constancia de uno de estos parámetros y el cambio en los otros dos indica que ocurre uno u otro isoproceso en el gas. Dedicaremos este artículo a una respuesta detallada a las preguntas de que este es un proceso isocórico, en qué se diferencia de los cambios isotérmicos e isobáricos en los estados de un sistema de gas.
Gas ideal en física

Antes de responder a la pregunta de que se trata de un proceso isocórico, deberías conocer mejor el concepto de gas ideal. En física, se entiende como cualquier gas en el que la energía cinética media de sus partículas constituyentes supera con creces la energía potencial de su interacción, y las distancias entre estas partículas son varios órdenes de magnitud mayores que sus dimensiones lineales. En las condiciones indicadas, es posible, al realizarlos cálculos no tienen en cuenta la energía de interacción entre partículas (es igual a cero), y también se puede suponer que las partículas son puntos materiales que tienen una cierta masa m.
El único proceso que tiene lugar en un gas ideal es la colisión de partículas con las paredes del recipiente que contiene la sustancia. Estas colisiones se manifiestan en la práctica como la existencia de una cierta presión en el gas P.
Como regla general, cualquier sustancia gaseosa que consiste en moléculas relativamente inertes químicamente y que tiene baja presión y altas temperaturas puede considerarse un gas ideal con suficiente precisión para los cálculos prácticos.
Ecuación que describe un gas ideal
Por supuesto, estamos hablando de la ley universal de Clapeyron-Mendeleev, que debe entenderse bien para entender que este es un proceso isocórico. Entonces, la ecuación de estado universal tiene la siguiente forma:
PV=norteRT.
Es decir, el producto de la presión P y el volumen de gas V es igual al producto de la temperatura absoluta T y la cantidad de sustancia en moles n, donde R es el factor de proporcionalidad. La ecuación en sí fue escrita por primera vez por Emile Clapeyron en 1834, y en los años 70 del siglo XIX, D. Mendeleev reemplazó en ella un conjunto de valores constantes de una sola constante universal de gas R (8.314 J/(molK)).
De acuerdo con la ecuación de Clapeyron-Mendeleev, en un sistema cerrado el número de partículas de gas permanece constante, por lo que solo hay tres parámetros macroscópicos que pueden cambiar (T, Py V). Este último hecho subyace a la comprensión de los diversos isoprocesos que se discutirán a continuación.
¿Qué es un proceso isocórico?
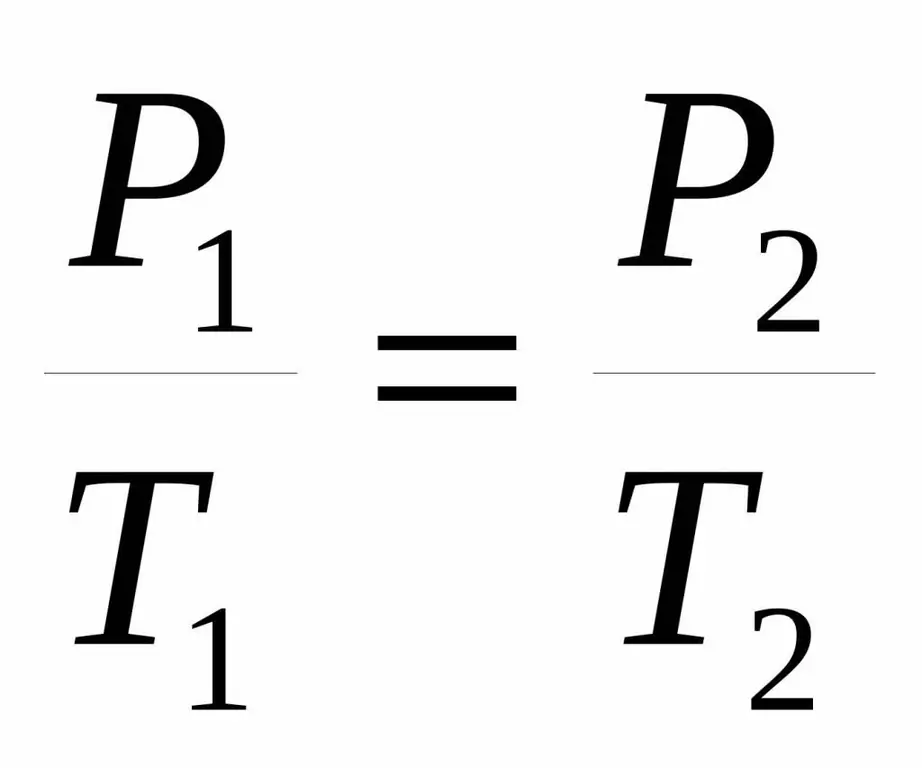
Este proceso se entiende como absolutamente cualquier cambio en el estado del sistema, en el que se conserva su volumen.
Si recurrimos a la ecuación de estado universal, podemos decir que en un proceso isocórico sólo cambian la presión y la temperatura absoluta en un gas. Para entender exactamente cómo cambian los parámetros termodinámicos, escribimos la expresión matemática correspondiente:
P / T=const.
A veces esta igualdad se da en una forma ligeramente diferente:
P1 / T1=P2 / T 2.
Ambas igualdades se denominan ley de Charles por el nombre de un científico francés que a finales del siglo XVIII obtuvo experimentalmente la dependencia indicada.

Si construimos un gráfico de la función P(T), entonces obtenemos una dependencia lineal, que se llama isocora. Cualquier isocoro (para todos los valores de n y V) es una línea recta.
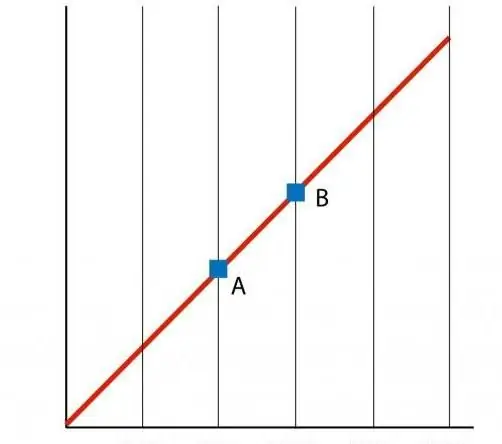
Descripción energética del proceso
Como se señaló, un proceso isocórico es un cambio en el estado de un sistema que tiene lugar en un sistema cerrado pero no aislado. Estamos hablando de la posibilidad de intercambio de calor entre el gas y el medio ambiente. En general, cualquier suministro de calor Q al sistema conduce a dos resultados:
- cambia la energía interna U;
- gasolinatrabaja A, expandiéndose o contrayéndose.
La última inferencia se escribe matemáticamente de la siguiente manera:
Q=U + A.
El proceso isocórico de un gas ideal, por su definición, no implica trabajo realizado por el gas, ya que su volumen permanece invariable. Esto significa que todo el calor suministrado al sistema se destina a aumentar su energía interna:
Q=U.
Si sustituimos la fórmula explícita de la energía interna en esta expresión, entonces el calor del proceso isocórico se puede representar como:
Q=z / 2nRT.
Aquí z es el número de grados de libertad, que está determinado por la naturaleza poliatómica de las moléculas que componen el gas. Para un gas monoatómico, z=3, para un gas diatómico - 5, y para un gas triatómico y más - 6. Aquí, bajo los grados de libertad, nos referimos a los grados de traslación y rotación.
Si comparamos la eficiencia de calentar un sistema de gas en procesos isocóricos e isobáricos, en el primer caso obtendremos la máxima eficiencia, ya que durante el cambio isobárico en el estado del sistema, el gas se expande y parte de la entrada de calor se gasta en hacer trabajo.
Proceso isobárico
Arriba hemos descrito en detalle que este es un proceso isocórico. Ahora digamos algunas palabras sobre otros isoprocesos. Comencemos con isobárico. En base al nombre, se entiende como la transición del sistema entre estados a presión constante. La ley de Gay-Lussac describe este proceso de la siguiente manera:
V / T=const.
Al igual que con la isócora, la isobara V(T) también representa una línea recta en el gráfico.
Parade cualquier proceso isobárico, conviene calcular el trabajo realizado por el gas, ya que es igual al producto de la presión constante por la variación de volumen.
Proceso isotérmico
Este es un proceso en el que la temperatura del sistema permanece constante. Está descrita por la ley de Boyle-Mariotte para un gas ideal. Es curioso notar que esta es la primera ley de los gases descubierta experimentalmente (segunda mitad del siglo XVII). Su notación matemática se ve así:
PV=const.
Los procesos isocóricos e isotérmicos difieren en términos de su representación gráfica, ya que la función P(V) es una relación hiperbólica, no lineal.
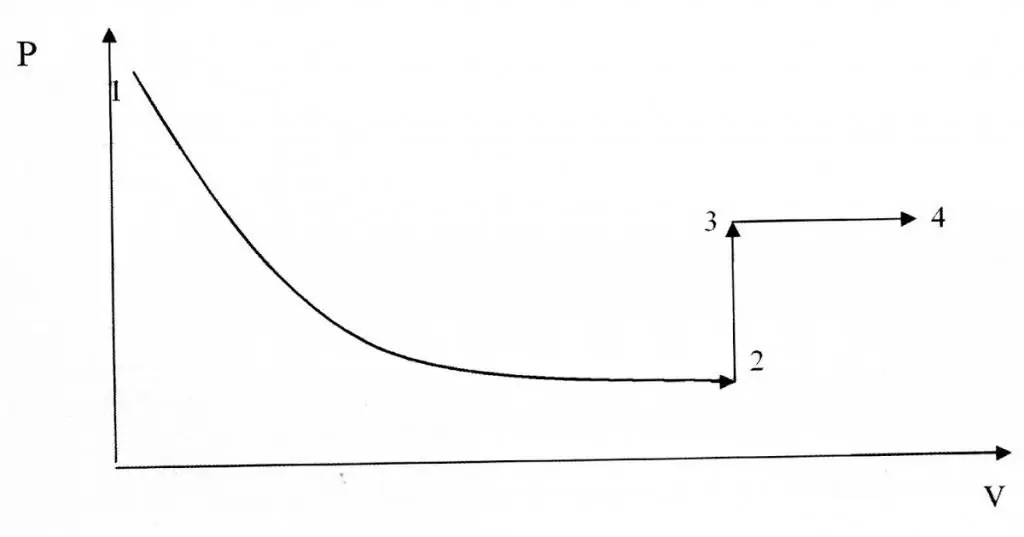
Ejemplo de resolución de problemas
Consolidemos la información teórica proporcionada en el artículo por su aplicación para resolver un problema práctico. Se sabe que el nitrógeno gaseoso puro estaba en un cilindro a una presión de 1 atmósfera y una temperatura de 25 °C. Después de calentar el cilindro de gas y medir la presión en él, resultó ser de 1,5 atmósferas. ¿Cuál es la temperatura del gas en el cilindro después del calentamiento? ¿En qué cantidad cambió la energía interna del gas si había 4 moles de nitrógeno en el globo?
Para responder a la primera pregunta, usamos la siguiente expresión:
P1 / T1=P2 / T 2.
De donde obtenemos:
T2=P2 / P1 T 1.
En esta expresión, la presión se puede sustituir en unidades arbitrariasmedidas, ya que se están encogiendo, y la temperatura está sólo en kelvins. Dicho esto, obtenemos:
T2=1,5 /1298,15=447,224 K.
La temperatura calculada en grados Celsius es 174 °C.
Dado que la molécula de nitrógeno es diatómica, el cambio en su energía interna durante el calentamiento se puede determinar de la siguiente manera:
ΔU=5 / 2nRΔT.
Sustituyendo los valores conocidos en esta expresión, obtendremos la respuesta a la segunda pregunta del problema: ΔU=+12.4 kJ.






