La pirámide junto con un prisma es un poliedro perfecto en el espacio tridimensional, sus características geométricas se estudian en la escuela secundaria. En este artículo, consideraremos qué son las pirámides, en qué elementos consisten y también caracterizaremos brevemente las pirámides correctas.
Pirámide de figuras geométricas
Desde el punto de vista de la geometría, la pirámide es una figura espacial, que consta de un polígono y varios triángulos. Conseguir esta figura es bastante sencillo. Para hacer esto, tome un polígono con n lados, luego elija un punto arbitrario en el espacio que no esté en el plano del polígono y conecte cada vértice del polígono a este punto. Obviamente, la figura así formada tendrá n triángulos conectados entre sí en un vértice.
Para visualizar la forma geométrica de la figura descrita, tomemos una foto.

Esto muestra una pirámide cuadrangular, cuya base escuadrilátero, y la superficie lateral está formada por cuatro triángulos que tienen un vértice común.
Elementos de la pirámide
Como todo poliedro, la pirámide está formada por tres tipos de elementos:
- bordes;
- tops;
- costillas.
Las caras son partes de planos que separan el volumen interno de una figura del espacio circundante. Si la base de la pirámide contiene un n-ágono, entonces el número de sus caras siempre es n+1. De estos, n lados son triangulares y un lado es la base n-gonal mencionada.
Los vértices son puntos donde se cruzan tres o más caras de una figura. La región base contiene n vértices, cada uno de los cuales está formado por dos caras triangulares y una base. El punto donde se juntan n lados triangulares se llama la parte superior de la pirámide. Por lo tanto, la figura bajo consideración consta de n+1 vértices.
Los bordes son líneas rectas que aparecen cuando dos caras se cruzan. Cada arista está delimitada por dos vértices en sus extremos. Cualquier pirámide con base de n-ágonos contiene 2n aristas. La mitad de este número, es decir, n, está formada únicamente por la intersección de triángulos laterales.
Posibles tipos de figuras
El nombre de la figura bajo consideración está determinado únicamente por el tipo de polígono en la base. Por ejemplo, si tiene tres esquinas y tres lados, la pirámide será triangular, si tiene cuatro, cuadrangular, y así sucesivamente.
El polígono puede ser convexo y cóncavo, así como de tipo regular y general. Todo esto también determina la apariencia de la pirámide.
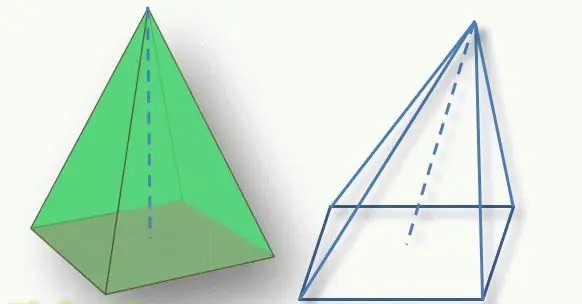
Un punto importante para determinar el tipo de figura es la posición de la parte superior de la pirámide en relación con su base. El segmento perpendicular trazado desde la parte superior hasta la base poligonal se llama altura de la figura. Si este segmento corta la base en su centro geométrico (para un triángulo, esta es la intersección de las medianas, para un cuadrilátero, la intersección de las diagonales), entonces la figura se llama línea recta. De lo contrario, hablan de una pirámide inclinada.
Si el n-ágono de la base es regular (triángulo equilátero, cuadrado, etc.) y la figura es recta, entonces se llama pirámide regular.
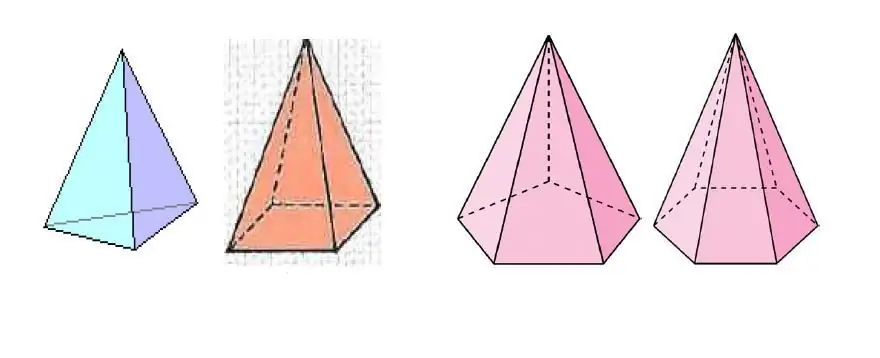
La imagen de arriba muestra varias pirámides, que difieren en el número de lados del polígono en la base.
Propiedades de las pirámides regulares
Estas pirámides difieren de otras figuras de esta clase por un alto grado de simetría. En este sentido, es conveniente realizar con ellos diversos cálculos geométricos, por ejemplo, de volumen o de superficie.
Una pirámide regular contiene un n-ágono en su base, cuyo área se determina únicamente a partir del conocimiento de la longitud de su lado. La superficie lateral de la figura está formada por n triángulos idénticos, que son equiláteros. Las aristas de una pirámide regular ubicada en la superficie lateral son iguales entre sí. El valor de la longitud de este borde se usa a menudo cuando se calcula la apotema de una figura y se determina el área de la superficie.
La altura de una pirámide regular es la segunda característica importante de la figura (la primera es la longitud de la aristajardines). La altura se utiliza para calcular el volumen.
Todo plano paralelo a la base, que corta las caras laterales de la pirámide, conduce a la formación de una sección poligonal. Es homotético con respecto al polígono base. La operación de división descrita conduce a la formación de toda una clase de figuras nuevas: pirámides regulares truncadas.
Las pirámides más famosas

Por supuesto, estas son las pirámides cuadrangulares regulares de los faraones egipcios. En un lugar llamado Giza, hay más de 100 de estos monumentos de piedra, la perfección del diseño y la precisión de los parámetros geométricos continúan asombrando a los científicos hasta el día de hoy. La más grande de ellas es la Pirámide de Keops, que tiene unos 146 metros de altura y unos 230 metros de largo.
Para qué sirvieron exactamente estas pirámides, así como por qué mecanismos y cuándo se construyeron, nadie lo sabe hasta el día de hoy.






