Como sabes, cualquier cantidad física pertenece a uno de dos tipos, es escalar o vectorial. En este artículo, consideraremos características cinemáticas como la velocidad y la aceleración, y también mostraremos hacia dónde se dirigen los vectores de aceleración y velocidad.
¿Qué es la velocidad y la aceleración?
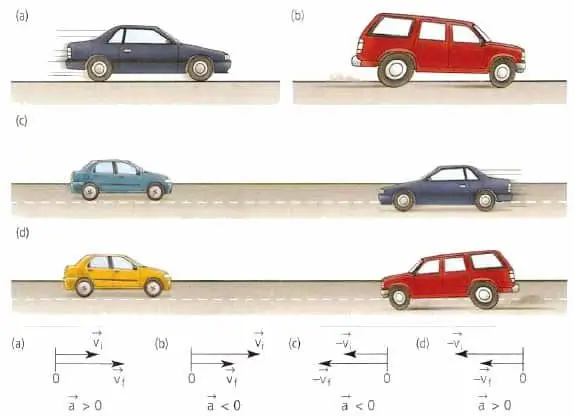
Las dos cantidades mencionadas en este párrafo son características importantes de cualquier tipo de movimiento, ya sea que se mueva un cuerpo en línea recta o a lo largo de una trayectoria curva.
La velocidad es la velocidad a la que cambian las coordenadas con el tiempo. Matemáticamente, este valor es igual a la derivada temporal de la distancia recorrida, es decir:
v¯=dl¯/dt.
Aquí el vector l¯ se dirige desde el punto inicial de la ruta hasta el punto final.
A su vez, la aceleración es la velocidad con la que la velocidad misma cambia en el tiempo. En forma de fórmula, se puede escribir así:
a¯=dv¯/dt.
Obviamente, tomando la segunda derivada devector de desplazamiento l¯ en el tiempo, también obtendremos el valor de la aceleración.
Como la velocidad se mide en metros por segundo, la aceleración, según la expresión escrita, se mide en metros por segundo al cuadrado.

¿Dónde están los vectores de aceleración y velocidad?
En física, cualquier movimiento mecánico de un cuerpo suele caracterizarse por una determinada trayectoria. Este último es una curva imaginaria a lo largo de la cual el cuerpo se mueve en el espacio. Por ejemplo, una línea recta o un círculo son excelentes ejemplos de trayectorias de movimiento comunes.
El vector de velocidad del cuerpo siempre está dirigido en la dirección del movimiento, sin importar si el cuerpo frena o acelera, si se mueve en línea recta o siguiendo una curva. Hablando en términos geométricos, el vector velocidad se dirige tangencialmente al punto de la trayectoria en el que se encuentra actualmente el cuerpo.
El vector aceleración de un punto material o corporal no tiene nada que ver con la velocidad. Este vector está dirigido en la dirección del cambio de velocidad. Por ejemplo, para el movimiento rectilíneo, el valor a¯ puede coincidir en la dirección con v¯ o ser opuesto a v¯.
Fuerza que actúa sobre el cuerpo y aceleración
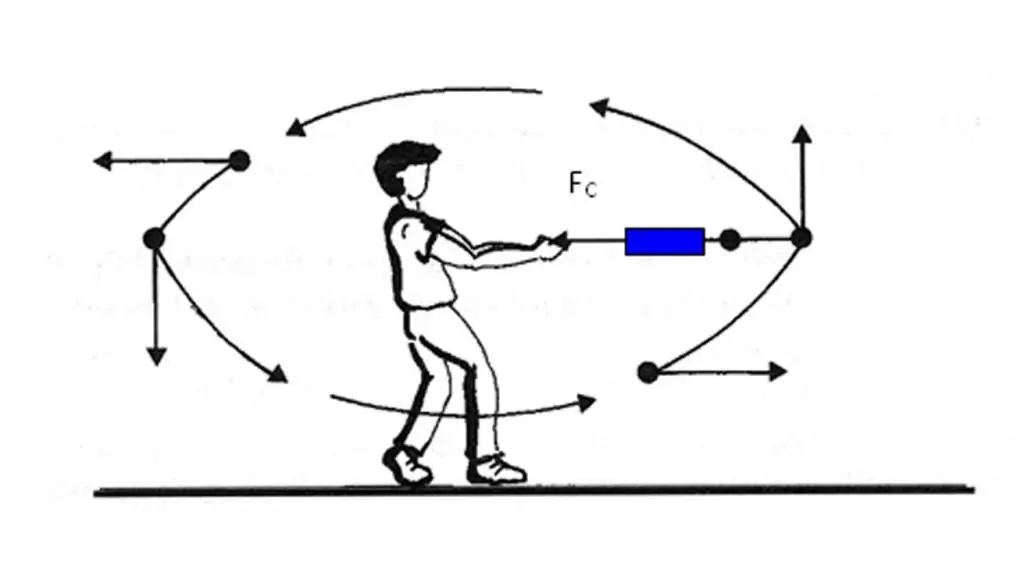
Hemos encontrado que el vector aceleración del cuerpo está dirigido hacia el cambio del vector velocidad. Sin embargo, no siempre es fácil determinar cómo cambia la velocidad en un punto dado de la trayectoria. Además, para determinar el cambio de velocidad, es necesario realizar la operacióndiferencias vectoriales. Para evitar estas dificultades a la hora de determinar la dirección del vector a¯, existe otra forma de averiguarlo rápidamente.
A continuación se muestra la famosa y conocida ley de Newton para todos los estudiantes:
F¯=ma¯.
La fórmula muestra que la causa de la aceleración en los cuerpos es la fuerza que actúa sobre ellos. Como la masa m es un escalar, el vector fuerza F¯ y el vector aceleración a¯ tienen la misma dirección. Este hecho debe recordarse y aplicarse en la práctica siempre que sea necesario determinar la dirección de la cantidad a¯.
Si varias fuerzas diferentes actúan sobre el cuerpo, entonces la dirección del vector aceleración será igual al vector resultante de todas las fuerzas.
Movimiento circular y aceleración
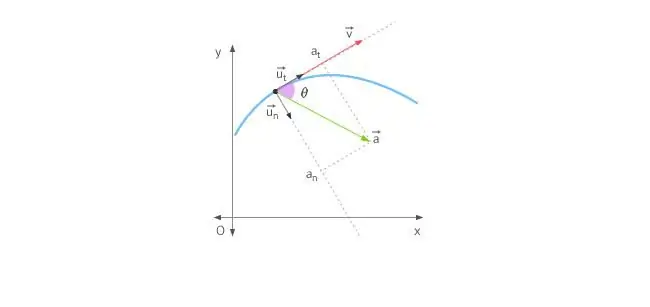
Cuando un cuerpo se mueve en línea recta, la aceleración se dirige hacia adelante o hacia atrás. En el caso del movimiento circular, la situación se complica por el hecho de que el vector velocidad cambia constantemente de dirección. En vista de lo anterior, la aceleración total está determinada por sus dos componentes: aceleraciones tangenciales y normales.
La aceleración tangencial se dirige exactamente igual que el vector de velocidad, o contra él. En otras palabras, esta componente de aceleración se dirige a lo largo de la tangente a la trayectoria. La aceleración tangencial describe el cambio en el módulo de la propia velocidad.
La aceleración normal se dirige a lo largo de la normal al punto dado de la trayectoria, teniendo en cuenta su curvatura. En el caso de movimiento circular, el vector de esta componente indicaal centro, es decir, la aceleración normal se dirige a lo largo del radio de rotación. Este componente a menudo se denomina centrípeto.
La aceleración total es la suma de estos componentes, por lo que su vector se puede dirigir arbitrariamente con respecto a la línea circular.
Si el cuerpo gira sin cambiar la velocidad lineal, entonces solo hay un componente normal distinto de cero, por lo que el vector de aceleración completo se dirige hacia el centro del círculo. Tenga en cuenta que este centro también se ve afectado por una fuerza que mantiene el cuerpo en su trayectoria. Por ejemplo, la fuerza gravitatoria del Sol mantiene a nuestra Tierra y a otros planetas en sus órbitas.






