La regla de Titius-Bode (a veces llamada simplemente ley de Bode) es la hipótesis de que los cuerpos en algunos sistemas orbitales, incluido el Sol, giran a lo largo de semiejes dependiendo de la secuencia planetaria. La fórmula sugiere que, extendiéndose hacia afuera, cada planeta estará aproximadamente el doble de lejos del Sol que el anterior.
La hipótesis predijo correctamente las órbitas de Ceres (en el cinturón de asteroides) y Urano, pero no pudo determinar la órbita de Neptuno y finalmente fue reemplazada por la teoría de la formación del sistema solar. Lleva el nombre de Johann Daniel Titius y Johann Elert Bode.

Orígenes
La primera mención de una serie que se aproxima a la ley de Bode se puede encontrar en Elements of Astronomy de David Gregory, publicado en 1715. En él dice: “… suponiendo que la distancia del Sol a la Tierra se divida en diez partes iguales, de las cuales la distancia de Mercurio será unas cuatro, de Venus siete, de Marte quince, de Júpiter cincuenta y dos, y de Saturno noventa y cinco . Una sugerencia similar, probablemente inspirada por Gregory, aparece en un trabajo publicado por Christian Wolff en 1724.
En 1764, Charles Bonnet, en su libro Contemplation of Nature, decía: "Conocemos los diecisiete planetas que componen nuestro sistema solar [es decir, los planetas principales y sus satélites], pero no estamos seguros de que ya no están". A esto, en su traducción de 1766 de la obra de Bonnet, Johann Daniel Titius añadió dos párrafos propios al final de la página 7 y al principio de la página 8. El nuevo párrafo interpolado no se encuentra en el texto original de Bonnet: ni en el italiano ni traducciones al inglés de la obra.
Descubrimiento de Titius
Hay dos partes en el texto intercalado de Titius. El primero explica la secuencia de distancias planetarias del Sol. También contiene algunas palabras sobre la distancia del Sol a Júpiter. Pero este no es el final del texto.
Vale la pena decir algunas palabras sobre la fórmula de la regla de Titius-Bode. Presta atención a las distancias entre los planetas y descubre que casi todos ellos están separados entre sí en una proporción correspondiente a sus tamaños corporales. Divide la distancia del Sol a Saturno por 100 partes; luego Mercurio está separado por cuatro de tales partes del Sol; Venus - en 4 + 3=7 de esas partes; Tierra - por 4+6=10; Marte - por 4+12=16.
Pero tenga en cuenta que de Marte a Júpiter hay una desviación de esta progresión tan precisa. Un espacio de 4+24=28 de tales partes sigue a Marte, pero hasta ahora no se ha descubierto un solo planeta allí. Pero, ¿debería el Lord Arquitecto dejar este lugar vacío? Nunca. Asi quesupongamos que este espacio pertenece sin duda a las lunas aún no descubiertas de Marte, y añadimos que quizás Júpiter todavía tenga algunas lunas más pequeñas a su alrededor que aún no han sido vistas por ningún telescopio.

Ascenso del Bode
En 1772, Johann Elert Bode, a la edad de veinticinco años, completó la segunda edición de su compendio astronómico Anleitung zur Kenntniss des gestirnten Himmels ("Guía para el conocimiento del cielo estrellado"), al que agregó la siguiente nota al pie, originalmente sin fuente, pero anotada en versiones posteriores. En las memorias de Bode se puede encontrar una referencia a Titius con un claro reconocimiento de su autoridad.

Opinión Bode
Así es como suena la regla de Titius-Bode en la presentación de este último: si la distancia del Sol a Saturno se toma igual a 100, entonces Mercurio está separado del Sol por cuatro partes. Venus - 4+3=7. Tierra - 4+6=10. Marte - 4+12=16.
Ahora hay una brecha en esta progresión ordenada. Después de Marte sigue un espacio con un cálculo de 4+24=28, en el que aún no se ha visto un solo planeta. ¿Podemos creer que el Fundador del universo dejó este espacio vacío? Por supuesto no. De aquí llegamos a la distancia de Júpiter en forma de cálculo 4+48=52 y, finalmente, a la distancia de Saturno - 4+96=100.

Estas dos declaraciones con respecto a toda tipología específica y radios orbitales parecen provenir de la antigüedadastronomía. Muchas de estas teorías datan de antes del siglo XVII.
Influencia
Titius fue alumno del filósofo alemán Christian Freiherr von Wolff (1679-1754). La segunda parte del texto insertado en el trabajo de Bonnet se basa en el trabajo de 1723 de von Wolff, Vernünftige Gedanken von den Wirkungen der Natur.
La literatura del siglo XX atribuye la autoría de la regla de Titius-Bode a un filósofo alemán. Si es así, Titius podría aprender de él. James Gregory escribió otra referencia más antigua en 1702 en su Astronomiae Physicae et geometricae Elementa, donde la secuencia de distancias planetarias 4, 7, 10, 16, 52 y 100 se convirtió en una progresión geométrica de la proporción 2.
Esta es la fórmula más cercana a Newton, y también se encuentra en los escritos de Benjamin Martin y Thomas Ceard años antes de que se publicara el libro de Bonnet en Alemania.
Trabajos adicionales e implicaciones prácticas
Titius y Bode esperaban que la ley condujera al descubrimiento de nuevos planetas y, de hecho, el descubrimiento de Urano y Ceres, cuya distancia concuerda bien con la ley, contribuyó a su aceptación por parte del mundo científico.
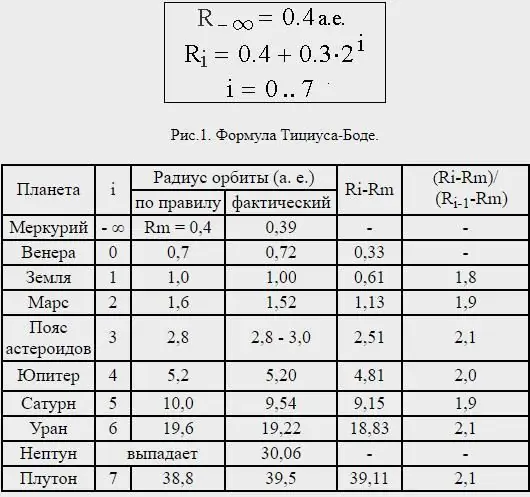
Sin embargo, la distancia de Neptuno era muy inconsistente y, de hecho, Plutón, que ahora no se considera un planeta, se encuentra a una distancia promedio que corresponde aproximadamente a la ley de Titius-Bode predicha para el próximo planeta fuera de Urano.
La ley publicada originalmente fue satisfecha aproximadamente por todos los planetas conocidos, Mercurio y Saturno, con una brecha entrecuarto y quinto planetas. Esta figura se consideró interesante, pero no de gran importancia, hasta el descubrimiento de Urano en 1781, que encaja en la serie.
Basándose en este descubrimiento, Bode solicitó la búsqueda de un quinto planeta. Ceres, el objeto más grande del cinturón de asteroides, fue encontrado en la posición predicha por Bode en 1801. La ley de Bode fue ampliamente aceptada hasta que se descubrió Neptuno en 1846 y se demostró que no se ajustaba a la ley.
Al mismo tiempo, una gran cantidad de asteroides descubiertos en el cinturón sacaron a Ceres de la lista de planetas. La ley de Bode fue discutida por el astrónomo y lógico Charles Sanders Peirce en 1898 como un ejemplo de razonamiento falaz.

Desarrollo del problema
El descubrimiento de Plutón en 1930 complicó aún más el problema. Aunque no coincidía con la posición predicha por la ley de Bode, se trataba de la posición predicha por la ley para Neptuno. Sin embargo, el posterior descubrimiento del cinturón de Kuiper, y en particular del objeto Eris, que es más masivo que Plutón pero no se ajusta a la ley de Bode, desacreditó aún más la fórmula.
Contribución de Serda
El jesuita Tomás Cerda impartió el famoso curso de astronomía en Barcelona en 1760 en la Real Cátedra de Matemáticas del Colegio de Sant Jaume de Cordelle (Imperial y Real Seminario de los Nobles de Cordell). En el Tratado de Cerdas aparecen las distancias planetarias, obtenidas aplicando la tercera ley de Kepler, con una precisión de 10-3.
Si tomamos como 10 la distancia a la Tierra yredondear a entero, se puede expresar la progresión geométrica [(Dn x 10) - 4] / [(Dn-1 x 10) - 4]=2, de n=2 a n=8. Y utilizando un movimiento circular uniforme ficticio a la anomalía de Kepler, los valores de Rn correspondientes a los ratios de cada planeta se pueden obtener como rn=(Rn - R1) / (Rn-1 - R1), dando como resultado 1,82; 1, 84; 1, 86; 1.88 y 1.90, donde rn=2 - 0.02 (12 - n) es una relación explícita entre la continuidad kepleriana y la ley de Titius-Bode, que se considera una coincidencia numérica aleatoria. El resultado del cálculo es cercano a dos, pero el dos bien puede considerarse como un redondeo del número 1, 82.

La velocidad promedio del planeta de n=1 a n=8 reduce la distancia al Sol y difiere del declive uniforme en n=2 para recuperarse de n=7 (resonancia orbital). Esto afecta la distancia del Sol a Júpiter. Sin embargo, la distancia entre todos los demás objetos en el marco de la notoria regla a la que se dedica el artículo también está determinada por esta dinámica matemática.
Aspecto teórico
No existe una explicación teórica sólida que sustente la regla de Titius-Bode, pero es posible que, dada la combinación de resonancia orbital y f alta de grados de libertad, cualquier sistema planetario estable tenga una alta probabilidad de repetir el modelo descrito en esta teoría por los dos científicos.
Debido a que esto puede ser una coincidencia matemática y no una "ley de la naturaleza", a veces se le llama regla en lugar de "ley". Sin embargo, el astrofísico Alan Boss argumenta que esto es simplementecoincidencia, y la revista científica planetaria Icarus ya no acepta artículos que intenten proporcionar versiones mejoradas de la "ley".
Resonancia orbital
La resonancia orbital de los principales cuerpos en órbita crea regiones alrededor del Sol que no tienen órbitas estables a largo plazo. Los resultados de la simulación de formación de planetas respaldan la idea de que es probable que un sistema planetario estable elegido al azar satisfaga la regla de Titius-Bode.

Dubrulle y Graner
Dubrulle y Graner demostraron que las reglas de distancia de la ley de potencias pueden ser una consecuencia de modelos de nubes colapsadas de sistemas planetarios que tienen dos simetrías: invariancia rotacional (la nube y su contenido son axisimétricos) e invariancia de escala (la nube y su contenido se ve igual en todas las escalas).
Esto último es una característica de muchos fenómenos que se cree que desempeñan un papel en la formación de planetas, como la turbulencia. La distancia del Sol a los planetas del sistema solar, propuesta por Titius y Bode, no fue revisada en el marco de los estudios de Dubrulle y Graner.






