El módulo de elasticidad es una cantidad física que caracteriza el comportamiento elástico de un material cuando se le aplica una fuerza externa en una dirección particular. El comportamiento elástico de un material significa su deformación en la región elástica.
Historia del estudio de la elasticidad de los materiales

La teoría física de los cuerpos elásticos y su comportamiento bajo la acción de fuerzas externas fue considerada en detalle y estudiada por el científico inglés del siglo XIX, Thomas Young. Sin embargo, el concepto mismo de elasticidad fue desarrollado allá por 1727 por el matemático, físico y filósofo suizo Leonhard Euler, y los primeros experimentos relacionados con el módulo de elasticidad se realizaron en 1782, es decir, 25 años antes del trabajo de Thomas Jung., del matemático y filósofo veneciano Jacopo Ricatti.
El mérito de Thomas Young radica en el hecho de que le dio a la teoría de la elasticidad un aspecto moderno y esbelto, que posteriormente se formalizó en forma de una ley de Hooke simple y luego generalizada.
Naturaleza física de la elasticidad
Todo cuerpo está formado por átomos, entre los cuales actúan las fuerzas de atracción y repulsión. El equilibrio de estas fuerzas esel estado y los parámetros de la materia bajo condiciones dadas. Los átomos de un cuerpo sólido, cuando se les aplican insignificantes fuerzas externas de tensión o compresión, comienzan a desplazarse, creando una fuerza de dirección opuesta e igual magnitud, que tiende a devolver los átomos a su estado inicial.
En el proceso de tal desplazamiento de átomos, la energía de todo el sistema aumenta. Los experimentos muestran que en pequeñas deformaciones la energía es proporcional al cuadrado de estas deformaciones. Esto quiere decir que la fuerza, al ser una derivada con respecto a la energía, resulta ser proporcional a la primera potencia de la deformación, es decir, depende linealmente de ella. Respondiendo a la pregunta de cuál es el módulo de elasticidad, podemos decir que este es el coeficiente de proporcionalidad entre la fuerza que actúa sobre el átomo y la deformación que esta fuerza provoca. La dimensión del módulo de Young es la misma que la dimensión de la presión (Pascal).
Límite elástico
Según la definición, el módulo de elasticidad indica cuánto esfuerzo se debe aplicar a un sólido para que su deformación sea del 100%. Sin embargo, todos los sólidos tienen un límite elástico igual al 1% de deformación. Esto significa que si se aplica una fuerza apropiada y el cuerpo se deforma en una cantidad inferior al 1%, luego de que termine esta fuerza, el cuerpo restaura exactamente su forma y dimensiones originales. Si se aplica demasiada fuerza, en la que el valor de deformación supera el 1%, después de la terminación de la fuerza externa, el cuerpo ya no recuperará sus dimensiones originales. En este último caso, se habla de la existencia de una deformación residual, que esevidencia de que se ha excedido el límite elástico del material.
Módulo de Young en acción
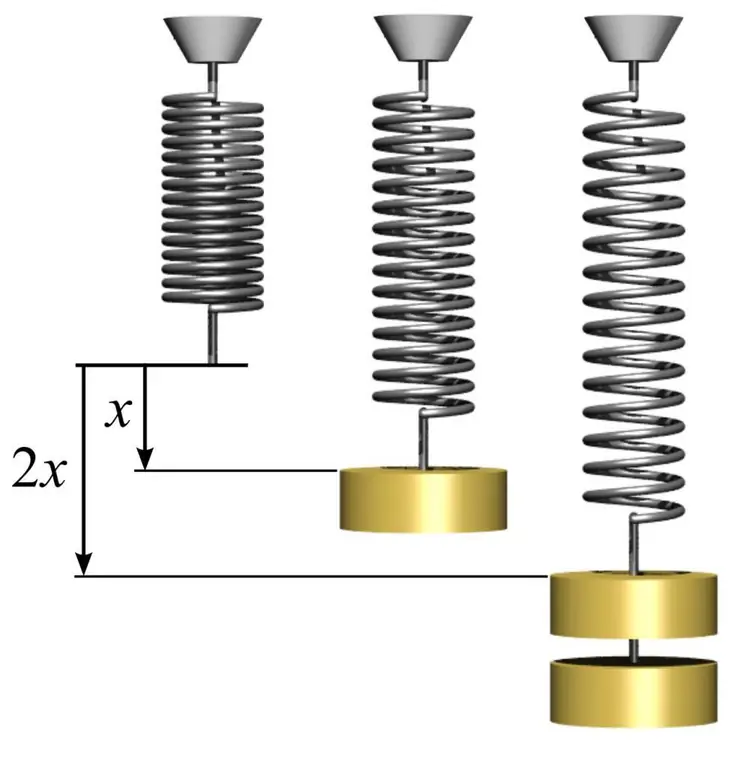
Para determinar el módulo de elasticidad, así como para entender cómo usarlo, puede dar un ejemplo simple con un resorte. Para hacer esto, debe tomar un resorte de metal y medir el área del círculo que forman sus bobinas. Esto se hace usando la fórmula simple S=πr², donde n es pi igual a 3.14 y r es el radio de la espiral del resorte.
Luego, mida la longitud del resorte l0 sin carga. Si cuelga cualquier carga de masa m1 en un resorte, aumentará su longitud a un cierto valor l1. El módulo de elasticidad E se puede calcular con base en el conocimiento de la ley de Hooke mediante la fórmula: E=m1gl0/(S(l 1-l0)), donde g es la aceleración de caída libre. En este caso, notamos que la cantidad de deformación del resorte en la región elástica puede exceder en gran medida el 1%.
Conocer el módulo de Young le permite predecir la cantidad de deformación bajo la acción de una tensión particular. En este caso, si colgamos otra masa m2 en el resorte, obtenemos el siguiente valor de deformación relativa: d=m2g/ (SE), donde d - deformación relativa en la región elástica.
Isotropía y anisotropía
El módulo de elasticidad es una característica de un material que describe la fuerza del enlace entre sus átomos y moléculas, sin embargo, un material en particular puede tener varios módulos de Young diferentes.
El hecho es que las propiedades de cada sólido dependen de su estructura interna. Si las propiedades son las mismas en todas las direcciones espaciales, entonces estamos hablando de un material isotrópico. Tales sustancias tienen una estructura homogénea, por lo que la acción de una fuerza externa en diferentes direcciones sobre ellas provoca la misma reacción en el material. Todos los materiales amorfos son isótropos, como el caucho o el vidrio.
La anisotropía es un fenómeno que se caracteriza por la dependencia de las propiedades físicas de un sólido o líquido en la dirección. Todos los metales y aleaciones basados en ellos tienen una u otra red cristalina, es decir, una disposición ordenada, en lugar de caótica, de núcleos iónicos. Para tales materiales, el módulo de elasticidad varía según el eje de acción de la tensión externa. Por ejemplo, los metales con simetría cúbica, como el aluminio, el cobre, la plata, los metales refractarios y otros, tienen tres módulos de Young diferentes.
Módulo de cortante
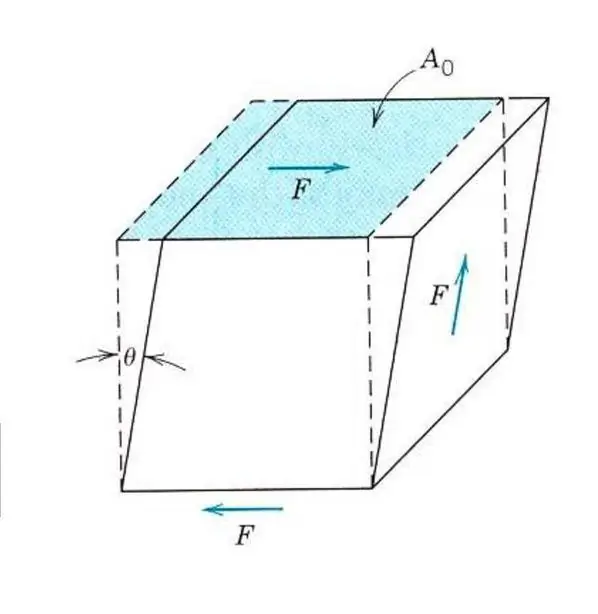
La descripción de las propiedades elásticas incluso de un material isotrópico no requiere el conocimiento del módulo de Young. Porque, además de la tensión y la compresión, el material puede verse afectado por esfuerzos cortantes o esfuerzos de torsión. En este caso, reaccionará de manera diferente a la fuerza externa. Para describir la deformación por corte elástico, se introduce un análogo del módulo de Young, el módulo de corte o el módulo de elasticidad del segundo tipo.
Todos los materiales resisten las tensiones de corte menos que la tensión o la compresión, por lo que el valor del módulo de corte para ellos es 2-3 veces menor que el valor del módulo de Young. Así, para el titanio, cuyo módulo de Young es igual a 107 GPa, el módulo de cortante essolo 40 GPa, para el acero estas cifras son 210 GPa y 80 GPa, respectivamente.
Módulo de elasticidad de la madera

La madera es un material anisotrópico porque las fibras de madera están orientadas en una dirección específica. Es a lo largo de las fibras que se mide el módulo de elasticidad de la madera, ya que es de 1 a 2 órdenes de magnitud menor a lo largo de las fibras. El conocimiento del módulo de Young para la madera es importante y se tiene en cuenta al diseñar estructuras de paneles de madera.
Los valores del módulo de elasticidad de la madera para algunos tipos de árboles se muestran en la siguiente tabla.
| Vista de árbol | Módulo de Young en GPa |
| Árbol de laurel | 14 |
| Eucalipto | 18 |
| Cedro | 8 |
| Pícea | 11 |
| Pino | 10 |
| Roble | 12 |
Cabe señalar que los valores dados pueden diferir hasta en 1 GPa para un árbol en particular, ya que su módulo de Young se ve afectado por la densidad de la madera y las condiciones de crecimiento.

Los módulos de corte para varias especies de árboles están en el rango de 1-2 GPa, por ejemplo, para el pino es de 1,21 GPa y para el roble de 1,38 GPa, es decir, la madera prácticamente no resiste los esfuerzos de corte. Este hecho debe tenerse en cuenta en la fabricación de estructuras portantes de madera, que están diseñadas para trabajar solo en tracción o compresión.
Características elásticas de los metales
Cuando se compara con el módulo de Young de la madera, los valores promedio de este valor para metales y aleaciones son un orden de magnitud mayor, como se muestra en la siguiente tabla.
| Metal | Módulo de Young en GPa |
| Bronce | 120 |
| Cobre | 110 |
| Acero | 210 |
| Titanio | 107 |
| Níquel | 204 |
Las propiedades elásticas de los metales que tienen una singonía cúbica se describen mediante tres constantes elásticas. Tales metales incluyen cobre, níquel, aluminio, hierro. Si un metal tiene una singonía hexagonal, ya se necesitan seis constantes para describir sus características elásticas.
Para los sistemas metálicos, el módulo de Young se mide con una deformación del 0,2 %, ya que pueden darse valores grandes en la región inelástica.






