En matemáticas, la suma (representada por el gran símbolo griego sigma) es un conjunto de sumandos de números. ¿Cual es la cantidad? Este es el resultado de tal acción. Si los números se suman uno tras otro de izquierda a derecha, el resultado intermedio es una suma parcial.
¿Cuál es la cantidad?
Los números a sumar pueden ser enteros, racionales, reales o complejos. Además de ellos, se pueden sumar otros tipos de valores: vectores, matrices, polinomios y, en general, elementos de cualquier grupo aditivo (o incluso un monoide).
Si el número de elementos de los términos es finito, entonces la suma siempre da un valor bien definido. La suma de una secuencia infinita de valores se llama serie. Su valor a menudo se puede determinar usando un límite (aunque a veces el valor puede ser infinito).
Secuencias
La suma de números [3, 7, 2, 1] se puede definir mediante una expresión cuyo valor es la suma de los dígitos incluidos en ella, por ejemplo 3 + 7 + 2 + 1=13. Dado que la sumaasociativamente, la suma no depende de cómo se agrupen los términos, por ejemplo, (3 + 7) + (2 + 1) y 3 + ((7 + 2) + 1) ambos equivalen a nueve, por lo que se suele prescindir de los paréntesis. La suma también es conmutativa, por lo que reorganizar los términos no cambia el valor de la suma. Tenga en cuenta que esta propiedad puede no funcionar para la suma infinita.

No existe una notación especial para sumar secuencias de este tipo. Solo hay un ligero matiz si hay menos de dos elementos. La suma de una secuencia de un miembro no contiene un signo más (es indistinguible de la forma del número en sí), y si no hay elementos en absoluto, entonces ni siquiera se puede escribir (sino que se puede denotar por su valor "0"). Sin embargo, si los términos de la secuencia están especificados por un patrón específico, como una función, entonces el operador de suma puede ser útil o incluso esencial.
Grabar
Para entender qué es una suma, también es necesario analizar su apariencia.
Para sumar una secuencia de números enteros del 1 al 100, a menudo se usa una expresión que incluye puntos suspensivos para indicar los miembros que f altan: 1 + 2 + 3 + 4 + … + 99 + 100. El patrón es bastante fácil de ver en este ejemplo. Sin embargo, para opciones más complejas, es necesario especificar exactamente la regla utilizada para encontrar el valor de los elementos, lo que se puede lograr utilizando el operador de suma "Σ". Usando este símbolo (sigma), puede aplicar la siguiente notación:
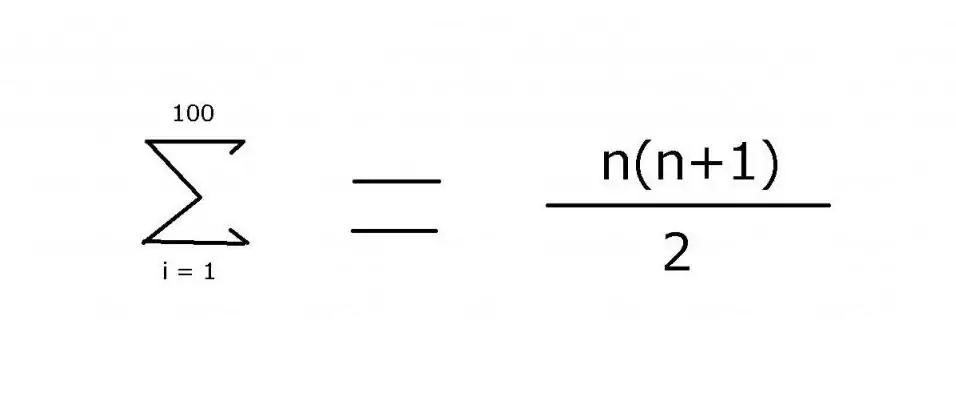
El valor de esta expresión es 5050. Se puede encontrar usando inducción matemática, que es de donde proviene la segunda parte de la fórmula.
Para diferentes secuencias, la fórmula cambiará. El proceso de grabación se reduce a buscar la preimagen de alguna secuencia infinita y luego describirla con una fórmula. Habiendo hecho esto, no es difícil entender cuál es la cantidad en un caso particular.
Cuando es necesario aclarar que los números se suman junto con sus signos (más o menos), se utiliza el término suma algebraica. Por ejemplo, en la teoría de circuitos eléctricos, las leyes de circuitos de Kirchhoff consideran la suma algebraica de corrientes en una red de conductores que se encuentran en un punto, dando signos opuestos a las corrientes que entran y salen de un nodo.






