En termodinámica, cuando se estudian las transiciones del estado inicial al final de un sistema, es importante conocer el efecto térmico del proceso. El concepto de capacidad calorífica está estrechamente relacionado con este efecto. En este artículo, consideraremos la cuestión de qué se entiende por capacidad calorífica isocórica de un gas.
Gas ideal
Un gas ideal es un gas cuyas partículas se consideran puntos materiales, es decir, no tienen dimensiones, pero sí masa, y en el que toda la energía interna consiste únicamente en la energía cinética del movimiento de las moléculas y átomos.
Cualquier gas real idealmente nunca satisfará el modelo descrito, ya que sus partículas todavía tienen algunas dimensiones lineales e interactúan entre sí usando enlaces débiles de van der Waals o enlaces químicos de otro tipo. Sin embargo, a bajas presiones y altas temperaturas, las distancias entre las moléculas son grandes y su energía cinética supera la energía potencial en docenas de veces. Todo esto hace posible aplicar con un alto grado de precisión el modelo ideal para gases reales.
Energía interna del gas
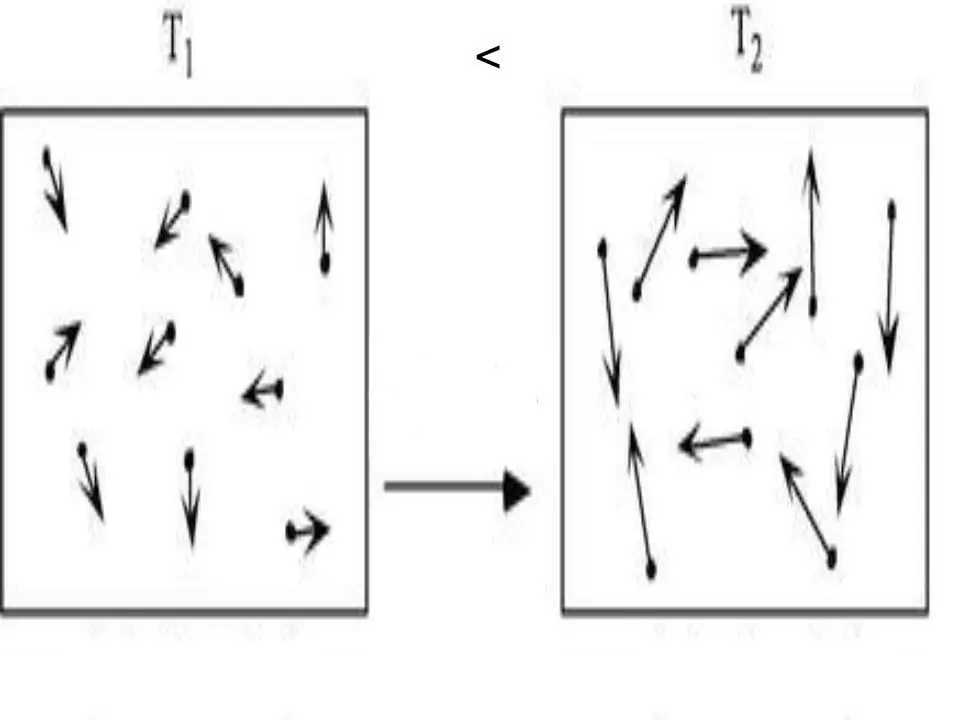
La energía interna de cualquier sistema es una característica física, que es igual a la suma de la energía potencial y cinética. Dado que la energía potencial puede despreciarse en los gases ideales, podemos escribir la igualdad para ellos:
T=Ek.
Donde Ek es la energía del sistema cinético. Usando la teoría cinética molecular y aplicando la ecuación de estado universal de Clapeyron-Mendeleev, no es difícil obtener una expresión para U. Se escribe a continuación:
U=z/2nRT.
Aquí T, R y n son la temperatura absoluta, la constante del gas y la cantidad de sustancia, respectivamente. El valor z es un número entero que indica el número de grados de libertad que tiene una molécula de gas.
Capacidad calorífica isobárica e isocórica
En física, la capacidad calorífica es la cantidad de calor que debe proporcionarse al sistema en estudio para calentarlo en un kelvin. La definición inversa también es cierta, es decir, la capacidad calorífica es la cantidad de calor que el sistema libera cuando se enfría un kelvin.
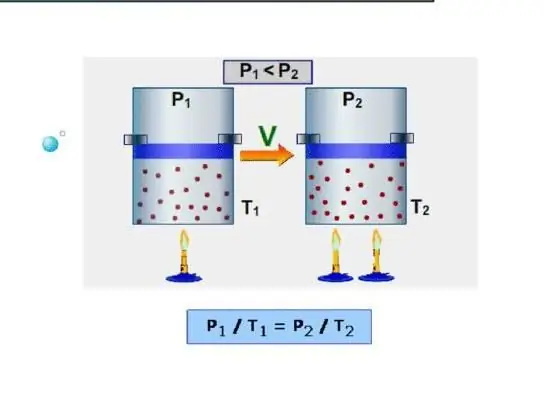
La forma más fácil para un sistema es determinar la capacidad calorífica isocórica. Se entiende como la capacidad calorífica a volumen constante. Dado que el sistema no realiza trabajo en tales condiciones, toda la energía se gasta en aumentar las reservas de energía interna. Denotemos la capacidad calorífica isocórica con el símbolo CV, entonces podemos escribir:
dU=CVdT.
Es decir, el cambio en la energía internasistema es directamente proporcional al cambio en su temperatura. Si comparamos esta expresión con la igualdad escrita en el párrafo anterior, llegamos a la fórmula de CV en un gas ideal:
СV=z/2nR.
Este valor es inconveniente de usar en la práctica, ya que depende de la cantidad de sustancia en el sistema. Por lo tanto, se introdujo el concepto de capacidad calorífica isocórica específica, es decir, un valor que se calcula por 1 mol de gas o por 1 kg. Denotemos el primer valor con el símbolo CV, el segundo - con el símbolo CV m. Para ellos, puedes escribir las siguientes fórmulas:
CV=z/2R;
CVm=z/2R/M.
Aquí M es la masa molar.
Isobárico es la capacidad calorífica mientras se mantiene una presión constante en el sistema. Un ejemplo de tal proceso es la expansión del gas en un cilindro debajo de un pistón cuando se calienta. A diferencia del proceso isocórico, durante el proceso isobárico, el calor suministrado al sistema se gasta para aumentar la energía interna y realizar trabajo mecánico, es decir:
H=dU + PdV.
La entalpía de un proceso isobárico es el producto de la capacidad calorífica isobárica y el cambio de temperatura en el sistema, es decir:
H=CPdT.
Si consideramos la expansión a una presión constante de 1 mol de gas, entonces la primera ley de la termodinámica se escribirá como:
CPdT=CV dT + RdT.
El último término se obtiene de la ecuaciónClapeyron-Mendeleiev. De esta igualdad se sigue la relación entre las capacidades caloríficas isobáricas e isocóricas:
CP=CV + R.
Para un gas ideal, la capacidad calorífica molar específica a presión constante siempre es mayor que la característica isocórica correspondiente por R=8, 314 J/(molK).
Grados de libertad de las moléculas y capacidad calorífica
Escribamos de nuevo la fórmula del calor específico isocórico molar:
CV=z/2R.
En el caso de un gas monoatómico, el valor z=3, ya que los átomos en el espacio solo pueden moverse en tres direcciones independientes.
Si estamos hablando de un gas que consta de moléculas diatómicas, por ejemplo, oxígeno O2 o hidrógeno H2, entonces, Además del movimiento de traslación, estas moléculas aún pueden girar alrededor de dos ejes mutuamente perpendiculares, es decir, z será igual a 5.
Para moléculas más complejas, use z=6. para determinar CV






